Area of Quadrant: A Detailed Explanation

Have you ever wondered how to calculate the space within a quadrant? Whether you’re crafting, designing, or tackling a math problem, mastering the Area of Quadrant can enhance your skills and boost your confidence. This fundamental concept in geometry might seem challenging at first, but with the right guidance, you'll find it much easier than you imagined. 

In this blog, we're here to unravel the mystery of the Area of Quadrant for everyone. We’ll simplify the formulas, walk you through practical examples, and provide handy tips along the way. With this newfound knowledge, your creative projects are bound to thrive! 

Table of Contents 

1) What is Quadrant? 

2) Area of Quadrant Formula 

3) How to Calculate the Area of Quadrant? 

4) Examples on Area of Quadrant 

5) Conclusion 

What is a Quadrant? 

A quadrant is one of the four equal parts into which a plane can be divided by two perpendicular lines, typically referred to as the x-axis and y-axis, in a coordinate system. In the context of geometry and circles, a quadrant refers to a quarter of a circle.  

Dividing a full circle into four equal parts by drawing two perpendicular diameters creates four quadrants. Essentially, a quadrant is a 90-degree arc or section of a circle. 

Quadrants are often encountered in both mathematical problems and real-life applications, such as in navigation and mapping, where the compass is divided into four quadrants to indicate direction. Similarly, when calculating the Area of Isosceles Triangle, understanding the different components like the base and height is essential, much like how each quadrant represents a specific range of directions. Additionally, concepts like the Volume of a Square play a crucial role in spatial calculations and geometric analysis.

Area of Quadrant Formula 

A quadrant's area can be derived from a full circle's area. The formula for the area of a circle is given by: 

where r is the radius of the circle. Since a quadrant is one-fourth of a full circle, the area of a quadrant is: 

This formula gives the area of the 90-degree section of the circle, which is a quadrant. It is derived by dividing the total circle area by four. Similarly, the Area of a Semi Circle is found by dividing the full circle area in half.

Get Precise Measurements – Discover the Easy Way to Find the Volume of a Cylinder!

How to Calculate the Area of Quadrant? 

To calculate the area of a quadrant, you need to follow a straightforward process: 

1) Determine the Radius: First, measure or determine the radius of the circle from which the quadrant is derived. The radius is the distance from the centre of the circle to any point on its circumference. 

2) Apply the Formula: Once you have the radius, use the formula for the area of a quadrant: 

3) Perform the Calculation: Plug in the value of the radius into the formula. First, square the radius, multiply it by π, and then divide the result by 4 to obtain the area of the quadrant. 

Example Calculation 

Let's go through an example. Suppose you have a circle with a radius of 10 cm and you want to find the area of one of its quadrants. 

Given: r =10 cm  

Area of the Quadrant: 

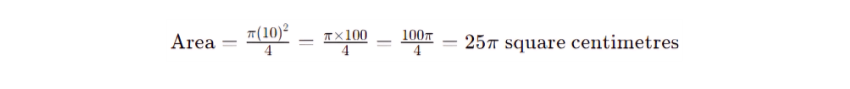
Thus, the area of the quadrant is 25π square centimetres, which approximately equals 78.54 square centimetres (using π ≈ 3.14159). 

Elevate your Engineering Skills! Join our Engineering Skills Training Today and Unlock your Full Potential with Hands-on Experience and Expert Guidance. 

Examples on Area of Quadrant 

Example 1: Small Circle 

Let's consider a smaller circle with a radius of 4 cm. To find the area of the quadrant: 

1) Given: r = 4 cm 

2) Area of the Quadrant: 

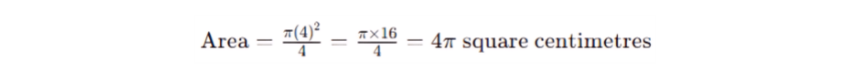
So, the area of this quadrant is 4π square centimetres, approximately 12.57 square centimetres. 

Example 2: Larger Circle 

For a larger circle with a radius of 20 cm: 

1) Given: r = 20 cm 

2) Area of the Quadrant: 

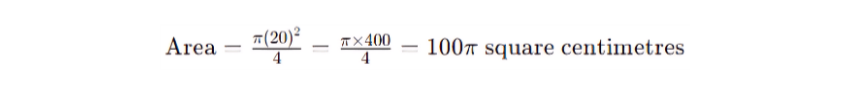
The area of this quadrant is 100π square centimetres, approximately 314.16 square centimetres. 

Example 3: Half Quadrant (Semicircle to Quadrant) 

If a semicircle is divided into two equal quadrants with a radius of 8 cm: 

1) Given: r = 8 cm 

2) Area of One Quadrant: 

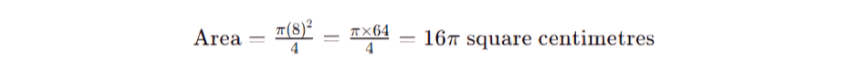
Thus, each quadrant has an area of 16π square centimetres, approximately 50.27 square centimetres. 

Unlock your True Potential by joining our Personal Development Training ! 

Conclusion 

The Area of Quadrant is a fundamental concept in geometry, derived from a full circle. This simple yet powerful formula, along with the Area of Square, has applications in multiple fields, from engineering and architecture to mathematics. With the step-by-step process outlined in this blog, you can determine the Area of Quadrant for any given circle.

Accelerate your Career! Join our Career Development Course and pave your way to Success in your Chosen Field.