Area of Square: A Detailed Explanation

Understanding the Area of a Square might seem straightforward, but it’s a crucial building block for many geometric calculations and practical applications. Whether you’re designing floor plans or creating art, knowing how to calculate the Area of a Square is essential. In this blog, we’ll delve into the concept of area, break down the specific formula for a square, and walk through examples to help you master this fundamental skill.  

Join us as we explore the fascinating world of square areas and equip you with the knowledge to tackle any square you encounter with confidence! 

Table of Contents 

1) What is Area? 

2) The Formula for the Area of a Square 

3) How to Calculate the Area of a Square 

4) Examples of Calculating the Area of a Square 

5) Common Core State Standards for Area 

6) Sample Problems for the Area of a Square 

7) Conclusion 

What is Area? 

Area is a fundamental geometric concept that measures the space within a two-dimensional shape's boundaries. Measured in square units (e.g., m², cm², in²), the area plays a crucial role in both practical and theoretical contexts. For instance, understanding the area helps determine how much space is available for furniture or how much paint is needed for a wall.  

The area is calculated using specific formulas for different shapes, with the square—featuring four equal sides—being among the simplest. Calculating the area of a square is a foundational skill, essential for tasks ranging from measuring garden space to estimating fabric size. Mastering this concept is valuable in both academic and real-world applications.
 

Formula for the Area of a Square 

The formula for calculating the Area of a Square is simple yet powerful: 

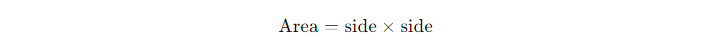
or more commonly written as: 

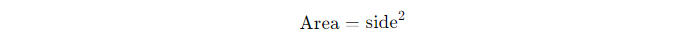
In this formula, "side" refers to the length of one of the square’s sides. As, all sides of a square are equal, you only need to know the length of one side to calculate the entire area. This formula is foundational in geometry and can be applied in various contexts, from academics to real-world problem-solving. 

How to Calculate the Area of a Square? 

Calculating the Area of a Square is a straightforward process using the formula mentioned above. Here’s how you can do it step by step: 

Measure the Length of a Side 

Begin by measuring one side of the square. Ensure the measurement is in the same units you wish to express the area (e.g., metres, centimetres). 

Apply the Formula 

Once you have the length of the side, plug it into the formula: 

Calculate the Result 

Multiply the side length by itself to find the area. The result will give you the area in square units. 

For example, if one side of the square is 5 metres, the area calculation would be: 

Take charge of your future! Join our Career Development Course today and unlock the skills and strategies to advance your professional journey.   

Examples of Calculating the Area of a Square 

To better understand the concept, let’s explore a few examples of how to calculate the Area of a Square using different methods. 

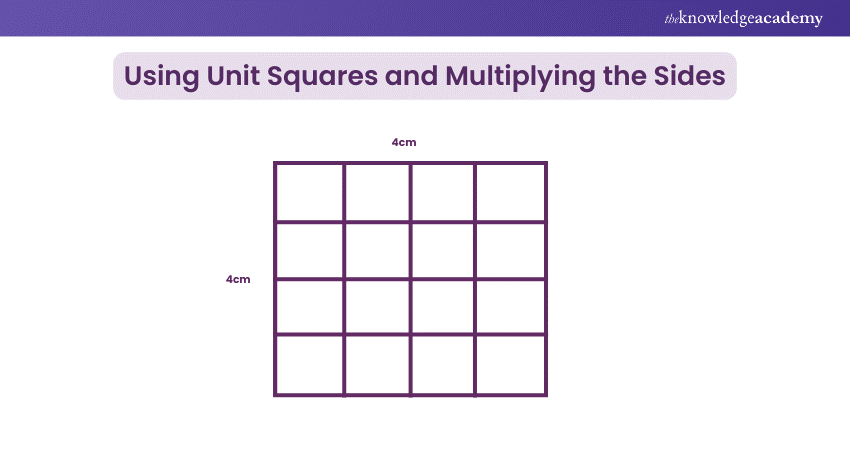
Using Unit Squares and Multiplying the Sides 

Example 1: Using Unit Squares 

Imagine a square with a side length of 4 centimetres. If you were to fill the square with unit squares (each 1 cm by 1 cm), you would count 16 unit squares inside the square. Therefore, the area of the square is 16 square centimetres. 

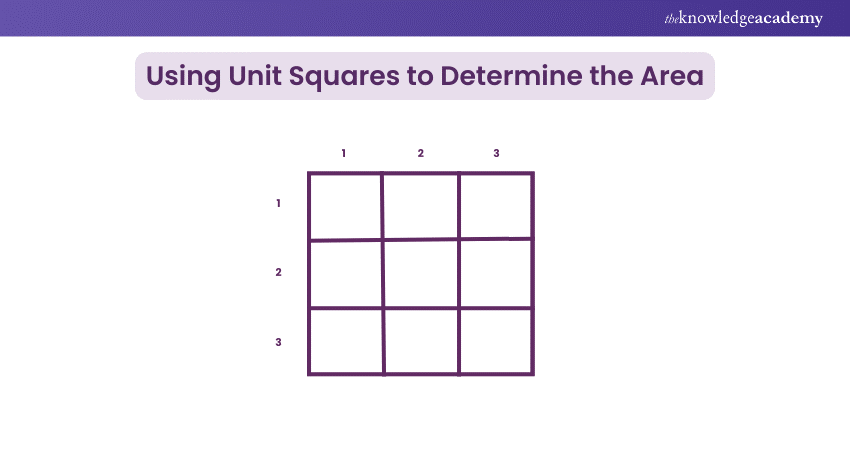
Using Unit Squares to Determine the Area 

In this method, you visualise the square as made up of smaller squares (unit squares). If each side of the square is three units long, you can arrange three rows of 3 unit squares each, resulting in 9 unit squares filling the square. Thus, the area is 9 square units. 

Multiplying the Sides to Find the Area 

Example 2: Multiplying the Sides 

Consider a square with a side length of 7 metres. Using the formula: 

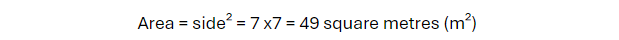
 This method is quicker and more efficient for finding the area, especially when dealing with larger numbers. 

Common Core State Standards for Area 

The Common Core State Standards (CCSS) highlight the importance of understanding areas from an early age. Starting in 3rd grade, students learn to measure area by counting unit squares (e.g., square cm, square m, square in, square ft). As they advance, they apply these calculations to various shapes, including squares, deepening their grasp of geometry and spatial reasoning.  

The standards aim to equip students with the ability to calculate areas and comprehend their practical uses, such as tiling floors, measuring land, or designing layouts. Mastering area calculations, particularly the area of squares, is essential for developing a solid mathematical foundation. 

Sharpen your skills. Train to Become a Top Engineer. Join our Engineering Skills Training now!   

Sample Problems for the Area of a Square 

To solidify your understanding, here are some sample problems to practice calculating the Area of a Square: 

Problem 1: 

A square garden has sides of 10 metres. Calculate the area of the garden. 

Solution: 

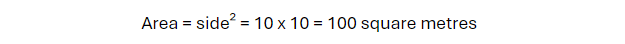
 Problem 2: 

A square tile has sides of 15 centimetres. What is the area of one tile? 

Solution: 

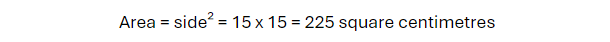
Problem 3: 

If a square field has an area of 64 square metres, what is the length of one side? 

Solution: 

To find the side length, take the square root of the area: 

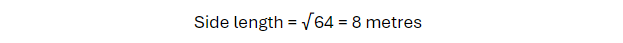
Conclusion 

Mastering the Fundamentals of the Area of a Square is more than just a mathematical exercise—it’s a skill with wide-ranging applications in everyday life. From architectural designs to artistic creations, understanding this fundamental concept empowers you to tackle various projects precisely and confidently. By grasping the formula and practising with examples, you can seamlessly integrate this knowledge into your toolkit. So, the next time you encounter a square, you’ll be ready to calculate its area with ease and accuracy. 

Take charge of your future! Join our Career Development Course today and unlock the skills and strategies to advance your professional journey.