Area of Trapezium: A Detailed Explanation

Imagine a shape that's partly rectangle and partly triangle with a unique twist—this is the Trapezium. Unlike regular shapes, a Trapezium has two parallel sides of different lengths. This makes its area calculation both fascinating and essential for various practical applications.  

However, we cannot always find the Area of a Trapezium by drawing unit squares. It requires a standard mathematical formula. This standard formula would help us in this situation. Continue reading this exciting blog to delve into the details of the Area of a Trapezium and its formula for decoding it. Let’s get to the paradigm of mathematical fun! 

Table of Contents 

1) What is Trapezium? 

2) Different Types of Trapeziums  

3) Area of Trapezium Formula 

4) Area of a Trapezium with a Parallelogram 

5)  Area of a Trapezium with a Triangle 

6) Examples of the Area of a Trapezium 

7) Conclusion 

What is a Trapezium?

A Trapezium is a four-sided polygon that falls under the category of Quadrilaterals. It has only one set of parallel sides.

 

The Trapezium's area is the space inside its boundaries, measured in square units like cm², m², mm², etc. 

 

 

Different Types of Trapeziums  

Trapeziums can be categorised based on their characteristics described below. These include the lengths of their sides or the measurements of their angles. 

1) Isosceles Trapezoid: An Isosceles Trapezoid has equal base angles, and its diagonals are the same length.

2) Scalene Trapezium: Scalene Trapezium has different base angles and diagonal lengths. 

Area of Trapezium Formula 

The area of a Trapezium can be calculated with the help of two parallel sides and the height of the Trapezium. The formula for calculating the area (A) of a Trapezium is:

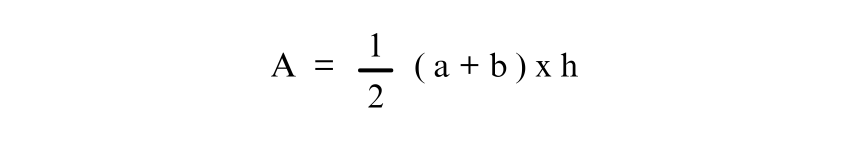
where: 

'a and ‘b’ are the parallel sides’ lengths (bases), 

'h’ is the perpendicular distance between the bases. 

There are primarily two methods to derive this formula: 

1) Using a Parallelogram: Rearranging two identical Trapeziums to form a Parallelogram’

2) Using a Triangle: Dividing the Trapezium into two Triangles and calculating their combined area.

Area of a Trapezium with a Parallelogram 

Consider two identical Trapeziums with bases ‘a’ and ‘b’ and height ‘h’. Let us assume ‘A’ as the area of each Trapezium. Now, turn the second Trapezium upside down and attach it to the first one. 

By joining the two Trapeziums, we can form a Parallelogram with an equal base of (a + b) and a height of ‘h’. 

Thus,

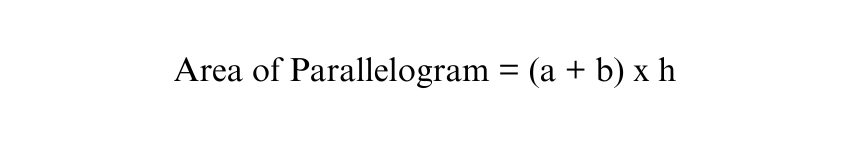
2) The area of the Parallelogram in terms of ‘A’ is the sum of the areas of the two Trapeziums:

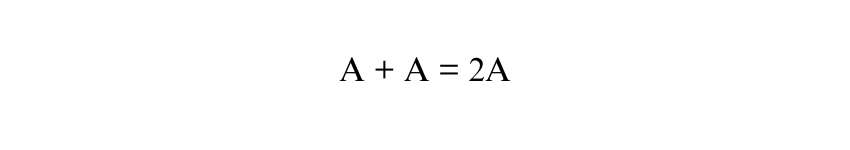
Therefore, the equation becomes:

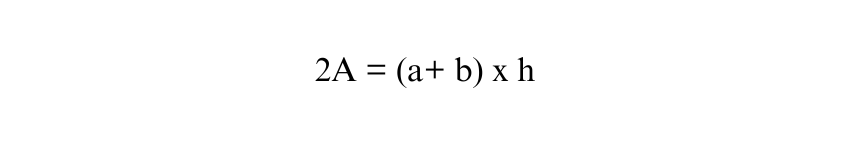
Learn the right techniques for prioritising tasks and increasing productivity with our Time Management Training – Register today!  

Area of a Trapezium with a Triangle 

To better understand how to derive the formula for the area of a Trapezium, let's explore a method using two identical Trapeziums. Follow these steps to get the formula for the area of a Trapezium: 

 

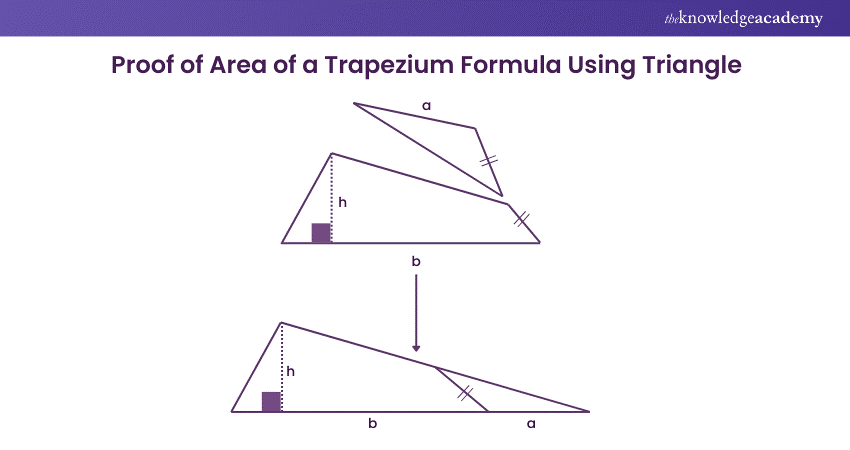
Step 1: Divide one of the non-parallel sides of the Trapezium into two equal parts. 

Step 2: Cut out a triangular section from the Trapezium. 

Step 3: Attach this triangular portion to the bottom of the shape. 

Now, the Trapezium is rearranged to form a Triangle, and the areas of both shapes are identical. The base of the triangle is (a + b), while the height remains h.  

Thus, the area of the Trapezium equals the area of the triangle, calculated as: 

Area of Trapezium = Area of triangle = ½ × base × height = ½ (a + b) × h. 

 

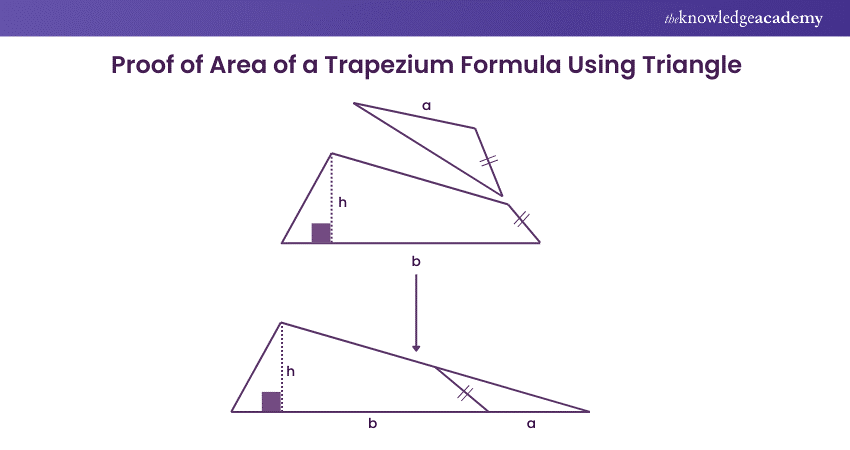
This rearrangement transforms the Trapezium into a triangle. From the diagram, it's clear that the areas of the original Trapezium and the newly formed triangle are the same. The triangle’s base is now equal to (a + b), and the height remains h. 

Thus, the area of the Trapezium is the same as the area of the triangle, which can be calculated using the formula: 

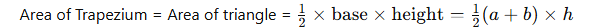
Learn cutting-edge strategic planning for business growth with our Strategic Planning and Thinking Course- Join now!

Examples of the Area of a Trapezium 

To help clarify the process of calculating the area, let’s look at a few practical examples. Below we have illustrated different scenarios for calculating the area of a Trapezium. 

Example 1: Determining the Area with Known Parallel Side Lengths and Height

If the lengths of the parallel sides are a = 8 units and b = 5 units, and the height h = 4 units, the area of the Trapezium can be calculated using the formula: 

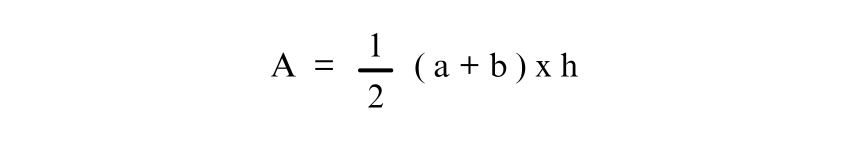
Substituting the given values:

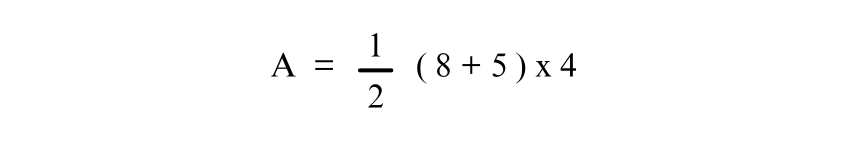
Simplifying

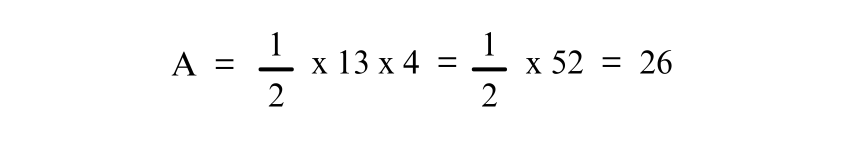
Thus, the area of the Trapezium is 26 square units.

Example 2: Finding the Area of a Trapezium with Unit Conversions

In this example, let’s say the parallel sides of the Trapezium are a = 500 cm and b = 300 cm, and the height is 2 meters. First, convert the height to centimetres: 

Since 1 meter = 100 centimetres, we convert 2 meters to centimetres:

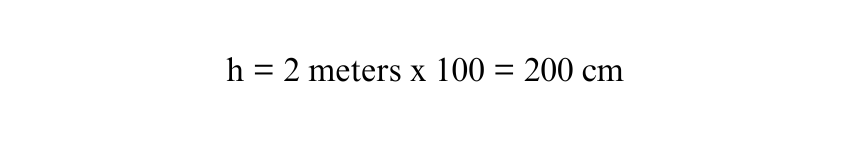
Now, using the formula for the area of the Trapezium:

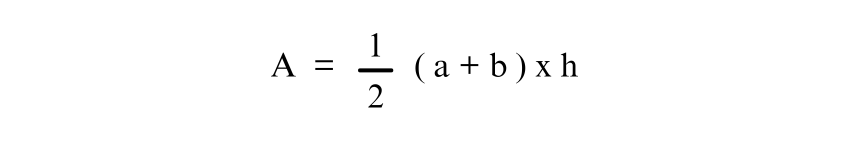
Substitute the known values:

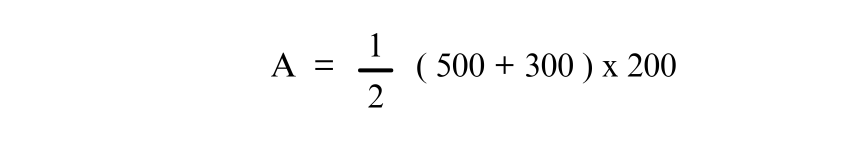
Simplifying:

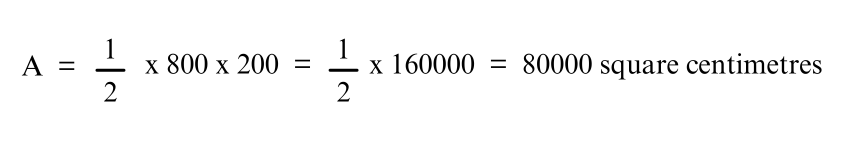
Thus, the area of the Trapezium is 80,000 square centimetres.

Example 3: Calculating the Height When the Area is Given

Suppose the area of the Trapezium is 45 square units, and the lengths of the parallel sides are a = 5 units and b = 3 units. To find the height h, use the formula and solve for h: 

Substitute the known values in the Trapezium formula, we get:

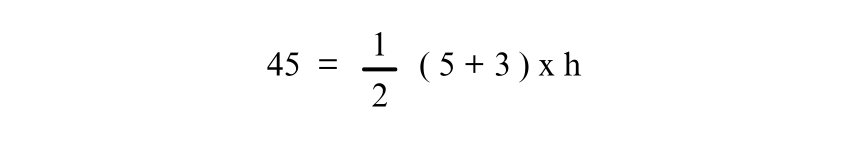
Simplifying the equation:

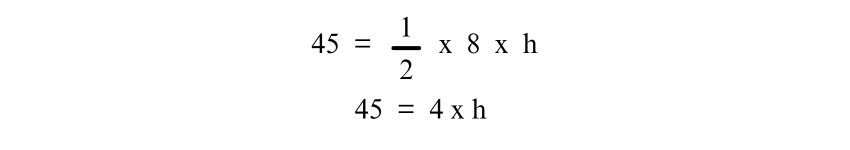
Now, solve for h by dividing both sides of the equation by 4:

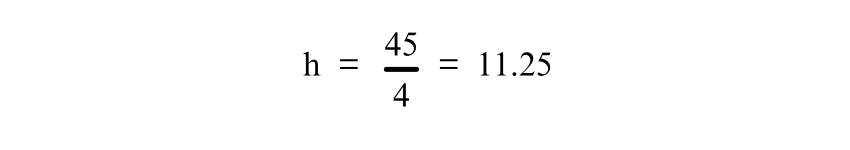
Thus, the height of the Trapezium is 11.25 units.

Example 4: Finding the Base Length When the Area is Known

If the area of the Trapezium is 64 square units, and the height is h = 4 units, with one of the parallel sides a = 10 units, find the other side b. Use the area formula and solve for b: 

Substitute the known values into the Trapezium area’s formula:

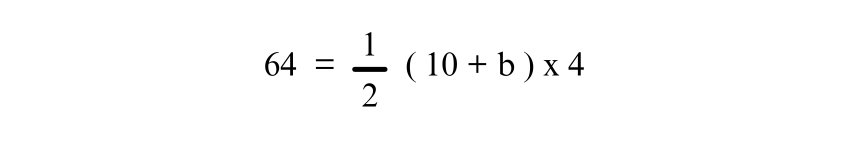
Simplifying the equation: 

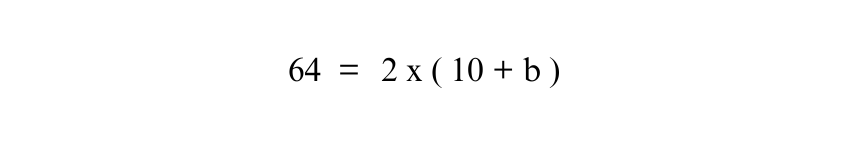
Now, divide both sides of equation by 2:

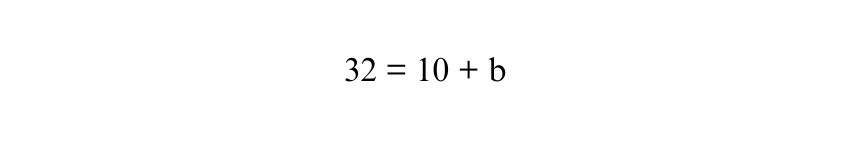
To find b, subtract 10 from both sides: 

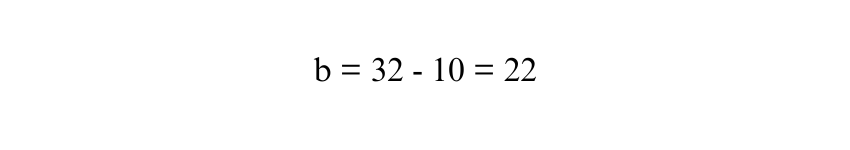
Thus, the length of the other parallel side b is 22 units.

What Is the Formula for the Height of a Trapezium Without Area?

To find the height of the Trapezoid, we must put all the other values into its area formula. This allows us to solve the problem of height when the area is not directly provided.

The basic formula for Trapezoid is 

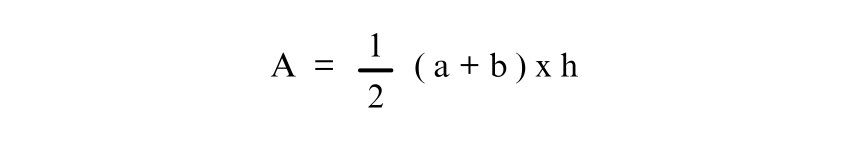
Where, a = long base

                 b= short base

                 h= height

Let’s suppose we have all other values besides height. Taking ‘h’ on one side, we multiply equation on both sides by 2 to eliminate the fraction,

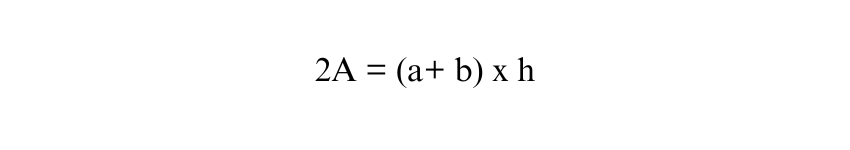
Now, solve for ’h’ by dividing both sides of the equation by (a+b) 

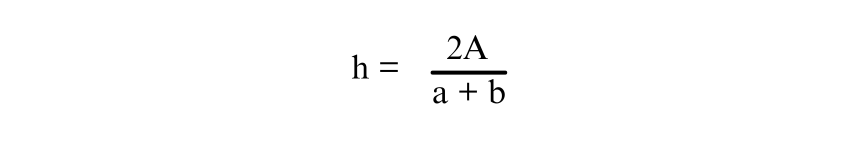
Thus, the formula for ‘h’ is 

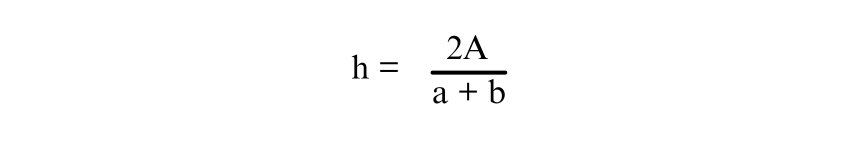
Learn proven stress reduction methods for success- join our Stress Management Course today!

Conclusion 

The Area of a Trapezium can be easily calculated using the formula ½ × (a + b) × h. Here, ‘a’ and ‘b’ are the parallel side lengths, and ‘h’ is the height. This versatile formula makes solving geometric problems involving Trapeziums easy, whether you're working with the sides, height, or area.

Transform your financial strategies with the right budgets- sign up for our Introduction to Managing Budgets today!