What is Dynamic Programming?

No matter how tricky a problem is, there's always a way to disassemble it into less tricky parts, like unweaving a web into individual strands. Nothing exemplifies this truth better in the modern world than Dynamic Programming (DP). This powerful technique used in Computer Science and Mathematics solves complex problems by breaking them into smaller, manageable pieces. Even better, DP stores the results of subproblems to avoid redundant calculations. This blog explores the brilliance behind What is Dynamic Programming by delving into its techniques, algorithms, benefits and more. So read on and learn what makes it a go-to option for everything from optimisation and scheduling to resource allocation!

Table of Contents

1) What is Dynamic Programming?

2) When to Use Dynamic Programming?

3) Exploring the Various Techniques of Dynamic Programming

4) Looking at the Steps to Solve Problems in Dynamic Programming

5) Dynamic Programming Algorithms

6) Example of Dynamic Programming

7) Advantages of Dynamic Programming

8) Disadvantages of Dynamic Programming

9) What is the Difference Between Dynamic Programming and Recursion?

10) What are the Two Problems That can be Solved Using Dynamic Programming?

11) Conclusion

Understanding What Dynamic Programming is

Dynamic Programming is a powerful algorithmic technique designed to solve problems by breaking them down into smaller ones. It overlaps subproblems and efficiently stores and reuses the solutions to those subproblems. The key idea behind DP is to avoid redundant computations by memorising intermediate results, which significantly enhances the algorithm's efficiency.

DP can be applied to several kinds of problems, particularly those with optimal substructure and overlapping subproblems. It is commonly used in various domains, including Algorithms, Artificial Intelligence, Economics, and Biology. 

There are two primary approaches to DP, namely the top-down approach (memoisation) and the bottom-up approach (tabulation). The top-down approach involves solving problems recursively while storing intermediate results in a data structure. The bottom-up approach involves building solutions iteratively, typically in a table or array. 

Dynamic Programming is a fundamental concept for solving complex problems efficiently. It plays an important role in optimising algorithms and finding optimal solutions in many real-world scenarios. 
 

 

 

When to Use Dynamic Programming?

Here are the two key features of a problem that are ripe for a Dynamic Programming approach:

1) Overlapping Subproblems: Dynamic Programming thrives on solving overlapping subproblems. These are smaller subproblems within a bigger problem that are solved independently and repeatedly. Solving and storing the results of the subproblems prevents redundant work and speeds up the overall solution. 

Here's an example of overlapping subproblems. Imagine that travel from City A to City B is common on several routes. Instead of calculating the distance between them every single time we’re mapping different routes, you can store the distance and reuse it whenever needed.

2) Optimal Substructure: Another important concept is the optimal substructure property, which means that the optimal solution to a bigger problem can be developed from the optimal solutions to smaller subproblems. This property allows us to simplify complex problems by breaking them down into smaller parts and solving them step by step.

Here's an example: Let's say you've determined the shortest path from City A to City B and the shortest path from City B to City C. The shortest path from City A to City C through City B could combine these two shortest routes.

Exploring the Various Techniques of Dynamic Programming

Dynamic Programming offers two primary approaches to solving problems. First is the top-down approach, which is often called ‘Memoisation’. Second is the bottom-up approach, known as ‘Tabulation’.

These approaches are distinct in their strategies but share the common goal of optimising solutions to problems with overlapping subproblems and optimal substructure. Here are the two approaches described in further detail:

Top-down Approach (Memoisation)

In Computer Science, solving problems often involves breaking them down into smaller subproblems. The top-down approach, also known as memoisation, is one such strategy. Here are some key points about the top-down approach:

1) Easy to Understand and Implement:

a) The top-down approach breaks complex problems into smaller parts, making it easier to identify what needs to be done.

b) Each step focuses on solving a smaller subproblem, which can be more manageable and reusable for similar problems.

2) On-demand Subproblem Solving:

a) By storing solutions for subproblems, the top-down approach allows users to query and reuse them as needed.

b) This flexibility helps address specific parts of a problem without recomputing everything.

3) Debugging Benefits:

a) Segmenting problems into smaller parts simplifies debugging. Users can pinpoint errors more easily.

However, there are some downsides to the top-down approach:

1) Recursion and Memory Usage:

a) The top-down approach relies on recursion, which consumes memory in the call stack.

b) Deep recursion can lead to performance issues, including stack overflow errors.

Bottom-up Approach (Tabulation) 

Now, let’s look closely into the bottom-up approach and explore its advantages:

1) Solving Subproblems First:

a) In the bottom-up method, we start by solving smaller subproblems before tackling larger ones.

b) By breaking down the problem into manageable pieces, we build a foundation for solving the overall problem.

2) Recursion Removal:

a) Unlike the top-down approach, which relies on recursion, the bottom-up approach avoids it altogether.

b) This eliminates the risk of stack overflow and reduces overhead from recursive function calls.

3) Memory Efficiency:

a) The absence of recursion allows for efficient memory usage.

b) We don’t need to maintain a call stack, leading to better memory management.

4) Time Complexity Reduction:

a) Recalculating the same values in recursion can be time-consuming.

b) The bottom-up approach avoids this by solving subproblems directly, resulting in improved time complexity.

Create efficient software solutions by signing up for our Coding Training now!

Looking at the Steps to Solve Problems in Dynamic Programming

Solving Dynamic Programming problems involves a systematic process to tackle complex computational challenges efficiently. The approach helps break down complex problems into manageable components and efficiently compute optimal solutions. This makes Dynamic Programming a powerful technique in algorithmic problem-solving.

Here are the key steps to solve Dynamic Programming problems: 

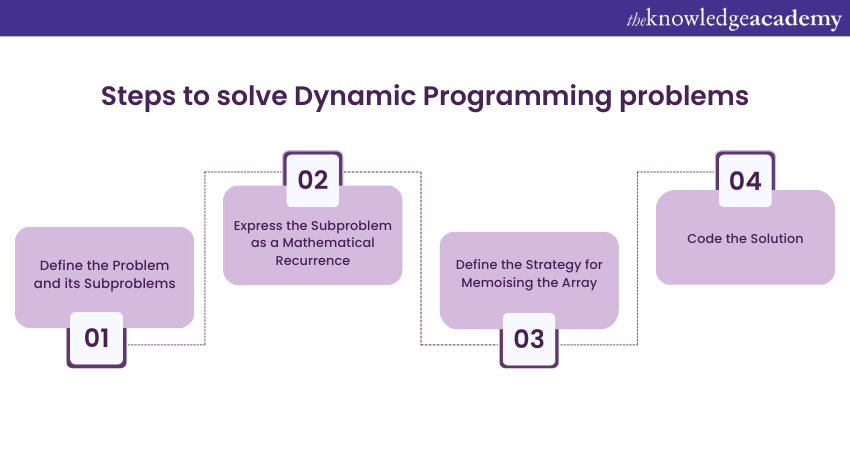
1) Define the Problem and its Subproblems

The first step in solving a DP problem is to understand the problem statement thoroughly. Identify the primary problem you need to solve and break it down into smaller, overlapping subproblems. 

Proceed to clearly define the subproblems that can be used to build the solution iteratively. These subproblems should have an optimal substructure. This means the best solution for the entire problem can be built from the optimal solutions of its subproblems.

For example, imagine yourself working on a problem related to finding the shortest path in a graph. Subproblems could involve finding the shortest path from one node to another within the same graph.

2) Express the Subproblem as a Mathematical Recurrence

Once you've identified the subproblems, express them as mathematical recurrences or recursive equations. These equations should describe how to construct the solution to a given subproblem using solutions to smaller subproblems. 

Furthermore, the recurrence relation should be structured in a way that relates the current subproblem to one or more smaller subproblems. This relation forms the foundation for building the DP solution.

Now, using mathematical notation, create a formula or equation that represents how the solution to a subproblem depends on the solutions to smaller subproblems. For example, in the Fibonacci sequence, F(n) = F(n-1) + F(n-2) is the recurrence relation. 

3) Define the Strategy for Memoising the Array

Decide whether you'll be using memoisation (top-down approach) or tabulation (bottom-up approach) to store and retrieve subproblem solutions. In memoisation, you'll create a data structure (usually an array or dictionary) to cache and retrieve the solutions to subproblems. 

Define the structure for memoisation. This means creating the array or data structure that will store the solutions to the subproblems. The size of the array is determined by the range of subproblems that need to be solved. 

Decide on a strategy to mark subproblems as unsolved. Typically, this involves using a special value (e.g., -1) or a boolean flag to indicate that a solution has not been computed yet.

4) Code the Solution

Implement the DP solution using the chosen approach (memoisation or tabulation). You can do this based on the mathematical recurrence and memoisation strategy defined in the previous steps. Start with the smallest subproblems and work your way up to the main problem. Compute and store the solutions for each subproblem in your memoisation array. 

Furthermore, loops or recursive functions can be used to iterate through the subproblems and calculate their solutions. Ensure that your code handles boundary cases, base cases, and termination conditions properly. Finally, the value stored in the main problem's cell of the memoisation array will be the optimal solution to the original problem. 

Dynamic Programming Algorithms

When Dynamic Programming algorithms are executed, they solve a problem by breaking it down into smaller parts until a solution is reached. They perform these tasks by finding the shortest path. Some of the primary Dynamic Programming algorithms in use are:

1) Floyd-Warshall Algorithm

The Floyd-Warshall algorithm uses Dynamic Programming to locate the shortest routes between every pair of vertices in a weighted graph, whether directed or undirected. It optimises estimates of the shortest routes between vertices by comparing potential routes through the graph. With minor modifications, one can reconstruct these paths.

This method includes two subtypes:

a) Behaviour with Negative Cycles: The algorithm can detect negative cycles by inspecting the diagonal path matrix for negative numbers, indicating a graph with a negative cycle. In such cycles, the sum of the edges is negative, preventing the shortest path between any pair of vertices. Exponentially large numbers are generated if a negative cycle occurs during execution.

b) Time Complexity: The Floyd-Warshall algorithm basically has three loops. Each of them has constant complexity, resulting in a time complexity of O(n^3). Here, n is the number of network nodes.

2) Bellman-Ford Algorithm

The Bellman-Ford Algorithm determines the shortest path in a weighted digraph from a specific source vertex to every other vertex. Unlike the Dijkstra’s algorithm, which may not produce a correct answer with negative edge weights, the Bellman-Ford algorithm can handle negative weights and produce a correct answer, though it is slower.

The Bellman-Ford algorithm works by relaxation, continuously replacing approximate distances with better ones until a solution is reached. It usually overestimates distances between vertices, updating values to reflect the minimum old value and the length of a newly found path. Upon finding a negative cycle this algorithm terminates and can be applied to cycle-cancelling techniques in network flow analysis.

3) Greedy Algorithms

An example of Dynamic Programming algorithms is greedy algorithms, which are also optimisation tools. The method solves a challenge by exploring optimum solutions to the subproblems and combining the findings to get the most optimal answer. Conversely, when greedy algorithms solve a problem, they search for a locally optimum solution to find a global optimum. They make a guess that seems optimum at the time but doesn't guarantee a globally optimum solution. This could prove costly down the road.

Example of Dynamic Programming 

Below is a code that demonstrates the concept of Dynamic Programming:

Explanation: The above code demonstrates the concept of Dynamic Programming by calculating the nth Fibonacci number by utilising a Dynamic Programming table. In the code, the ‘dp’ list stores the solutions to the sub-problems and the list is iteratively filled with a bottom-up approach.  

Build applications and solve computational problems by signing up for our Object-Oriented Fundamentals (OOP's) Course now! 

Advantages of Dynamic Programming 

Dynamic Programming (DP) is a problem-solving technique that has numerous advantages. It is an indispensable tool in various fields of Computer Science, Mathematics, economics, and beyond. Here is a list describing some of the advantages of Dynamic Programming: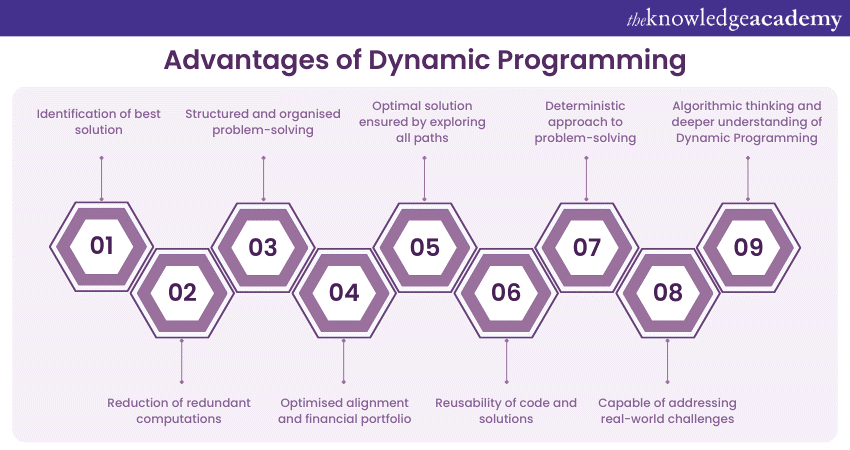

a) Optimisation: DP is primarily used to solve optimisation problems where the goal is to find the best solution among a set of possible solutions. It ensures that the optimal solution is identified efficiently. 

b) Efficiency: By storing and reusing solutions to overlapping subproblems, DP dramatically reduces redundant computations. This efficiency is especially valuable for solving complex problems in polynomial time rather than exponential time. 

c) Clarity and Structure: DP offers a structured and organised approach to problem-solving. It breaks down problems into smaller, more manageable subproblems, enhancing clarity in understanding and solving intricate challenges. 

h) Versatility: DP is a versatile technique that can be applied to different types of problems. It is used in shortest-path algorithms and string matching. Additionally, DP is crucial for sequence alignment and financial portfolio optimisation

i) Accuracy: DP ensures accuracy in solutions by considering all possible subproblems and exhaustively exploring all paths to find the optimal solution. It avoids heuristics that might lead to suboptimal or incorrect answers. 

j) Reusability: DP promotes the reusability of code and solutions. Once a subproblem is solved, its solution can be stored and reused in different contexts or for different parts of the problem. 

k) Deterministic: DP provides a deterministic approach to problem-solving, ensuring it always produces the same optimal result for a given set of inputs. This consistency guarantees the reliability of the solutions.

l) Real-world applications: DP is not just a theoretical concept. It has practical applications in fields like Computational Biology, Economics, Artificial Intelligence, and Computer Graphics. This versatility makes it invaluable for addressing real-world challenges.

m) Educational value: Learning and mastering DP helps individuals develop robust problem-solving skills and algorithmic thinking. It also provides a deeper understanding of Dynamic Programming and recursion in Computer Science and Mathematics.

Empower your skills with Programming languages by signing up for our Programming Training now! 

What is the Difference Between Dynamic Programming and Recursion?

Recursion involves solving a problem by dividing it into smaller subproblems and calling the same function to solve those subproblems. On the other hand, Dynamic Programming optimises the recursive approach by storing the results of subproblems in a table or by building up solutions bottom-up.

What are the Two Problems That can be Solved Using Dynamic Programming?

Two classic problems that can be solved with Dynamic Programming are:

1) Fibonacci Sequence: Calculating the nth Fibonacci number efficiently by storing previously computed values to avoid redundant calculations.

2) Knapsack Problem: Finding the maximum value that can be carried given a set of items with specific weights and values.

Conclusion 

In conclusion, Dynamic Programming is a potent problem-solving approach that simplifies complex challenges by breaking them down into manageable subproblems. This makes algorithms more efficient by storing solutions to these subproblems to avoid any redundant calculations. As pointed out in this blog, DP is widely used in fields like Computer Science, optimisation, and Data Analysis, making it a cornerstone for tackling computationally intensive tasks.

Do you want to learn how to work with looping and conditional statements? Register for our Python Course today!