We may not have the course you’re looking for. If you enquire or give us a call on 01344203999 and speak to our training experts, we may still be able to help with your training requirements.
Training Outcomes Within Your Budget!
We ensure quality, budget-alignment, and timely delivery by our expert instructors.

Statistics can sound intimidating, but what if we tell you, it all starts with three simple words: Mean Median Mode? They comprise a framework of approach to analysis of data; they assist in revealing patterns, in searching for the middle of information, and interpreting numbers in the real world. No matter if a learner, a worker, or someone who just wants to learn something about data, knowing these basics will be of big assistance.
In this blog, we will learn how to calculate the Mean Median Mode process one at a time. What you are to understand will include ungrouped and grouped data, applications, calculations, and differences. Read ahead to explore the world of data and get to know about how numbers speak for themselves.
Table of Contents
1) What are the Mean, Median, and Mode?
2) Steps to Calculate the Mean of a Data Set
3) Steps to Identify the Median
4) Steps to Find the Modal Value of a Data Set
5) Key Differences Between Mean, Median, and Mode
6) Conclusion
What are the Mean, Median, and Mode?
Mean, Median and Mode serve as measures of central tendency in statistics. They summarise a set of numbers to a single representative value, making it easier to analyse and interpret data.
1) Mean
The Mean, often called the average, is calculated by adding all the values in a data set and dividing them by the number of values.
1) Ungrouped Data
For ungrouped data, the Mean is calculated as:
Mean = Sum of all values ÷ Number of values Sum of all values ÷Number of values
Example: If the values are 2,4,6,8,10 the Mean is:
Mean= 2+4+6+8+10 / 5 = 6
2) Grouped Data
For grouped data, the Mean is calculated by using the formula:
Mean = (Σ f * x) / (Σ f)
Where f is the frequency of a class interval and x is the midpoint
Where:

Example: If we have the following grouped data:
|
Class Interval |
Frequency (f) |
Midpoint (x) |
f * x |
|
0-10 |
4 |
5 |
20 |
|
10-20 |
6 |
15 |
90 |
|
20-30 |
10 |
25 |
250 |
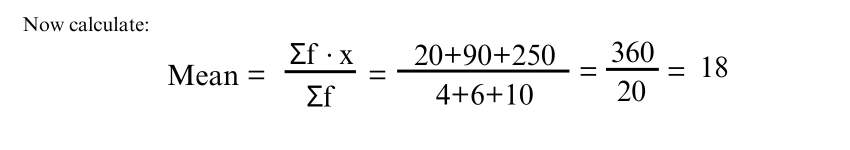
2) Median
The Median is the middle value that comes out when data is arranged in ascending order. It is a more robust measure when the data contains outliers.
1) Ungrouped Data
a) Arrange the data in order (ascending)
b) Odd Number of Values: The Median is the middle value
c) Even Number of Values: The Median is the Mean of the two middle values
Example: For 1,3,5,7,91, 3, 5, 7, 9 (odd):
Median = 5
For 1,3,5,7 (even): Median = 3+5 / 2 = 4
Transform your career with in-demand skills – join our Business Analyst Courses now!
2) Grouped Data
The formula for grouped data is:
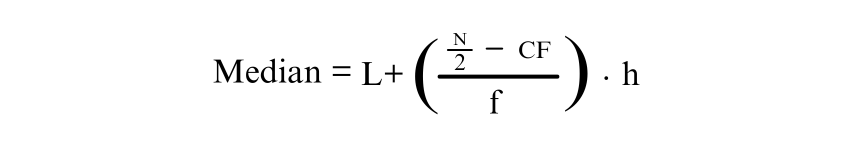
Where:

3) Mode
The Mode is the value that appears most frequently in a data set
1) Ungrouped Data
a) Identify the value(s) that occur most often
Example: For 2,2,3,4,4,4,5 the Mode = 4 (appears most frequently)
2) Grouped Data
The formula for the Mode is:
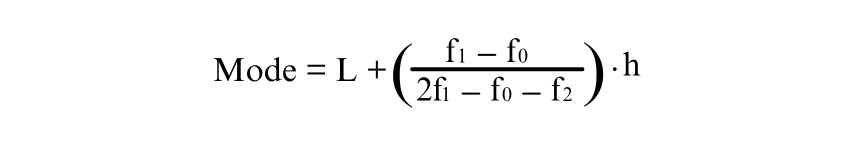
Where:

Steps to Calculate the Mean of a Data Set
The Mean is simply the average of all numbers in a data set
1) Add Up All the Values
Adding up all the values for the Mean:
a) This means summing up each number in your data set
Example: For the data 2,4,6,8:
2+4+6+8 = 20
2) Divide the Total by the Number of Values
Dividing the total by the number of values for Mean:
a) Take the total sum from Step 1 and divide it by the number of values in the set
Example: There are 4 values in the data set
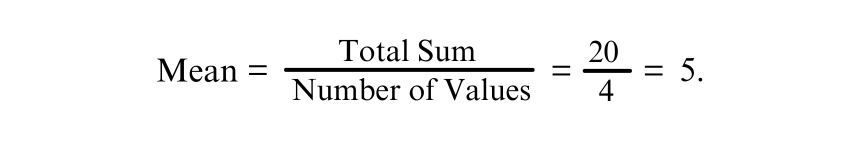
Answer: The Mean (average) of 2,4,6,8 is 5
Steps to Identify the Median
The Median is the middle value in a sorted data set. If the set has an even number of values, it’s the average of the two middle numbers.
1) Arrange Your Data in Order
Arranging the data in the order for the Median:
a) Sort all numbers in ascending order (from smallest to largest)
Example: Data set 7,3,5 → Sorted: 3,5,7
2) Find the Middle Value
Finding the middle values for the Median
If the number of values is odd:
a) The middle number is the Median
Example: For 3,5,7 → Median = 555
If the number of values is even:
a) Average the two middle numbers
Example: Data set 4,6,8,10:
Middle values = 6 and 8
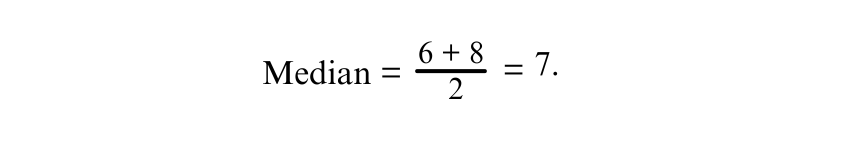
Answer: The Median is 7 for 4,6,8,10
3) Calculate the Mean of two Middle Values (if Necessary)
If a data set contains only four values, there isn't a single middle value when arranged in ascending order. For instance, consider the data set: 10, 12, 14, and 16. To find the Median, add the two middle values (12 and 14), resulting in 26. Then, divide this sum by 2 to get the Median value, which is 13.
Transform numbers into knowledge with our Mathematical Optimisation For Business Problems Course - Register today!
Steps to Find the Modal Value of a Data Set
The Mode is the number that occurs most frequently in the data set
1) Arrange the Data Set in Order
Arranging the data set in the order for Mode:
a) Organise the values from smallest to largest
Example: 5,3,3,4,6,3 → Sorted: 3,3,3,4,5,6
2) Identify the Value That Appears Most Frequently
Identifying the value that appears most frequently for Mode:
a) Look for the number that repeats the most
Example: In 3,3,3,4,5,6 the number 3 appears most often
Key Differences Between Mean, Median, and Mode
The following are the key differences between Mean, Median, and Mode:
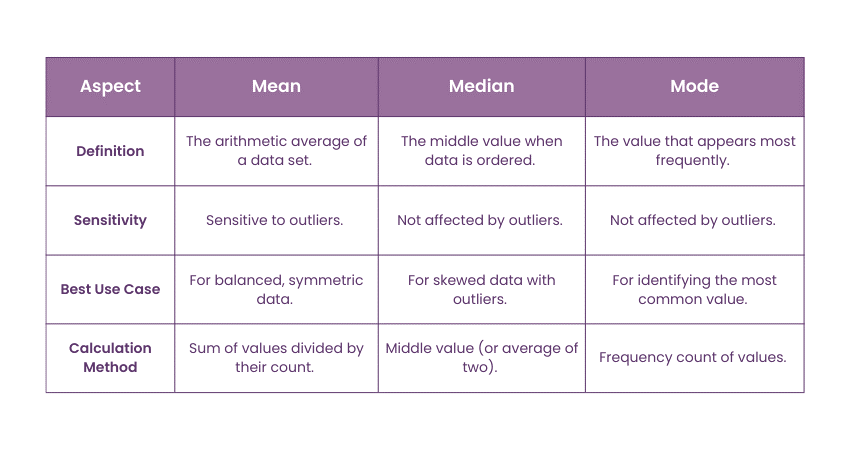
1) Definition:
a) Mean is the arithmetic average of a set of values, calculated by summing all the values and dividing by their count.
b) Median is the middle value in an ordered dataset or the average of the two central values if the dataset has an even number of entries.
c) Mode represents the value or values that occur most often within a dataset
2) Calculation:
a) Mean requires summing all data points and dividing by their total count
b) Median involves arranging the data in ascending order and identifying the central value(s).
c) Mode is determined by identifying the most frequently occurring value(s), requiring no arithmetic calculations.
3) Sensitivity to Outliers:
a) Mean is highly sensitive to outliers, which can skew its value significantly
b) Median is not affected by outliers and provides a better representation of central tendency for skewed data.
c) Mode is unaffected by outliers as it is based solely on frequency
4) Suitability for Data Types:
a) Mean is suitable for continuous or quantitative data
b) Median is ideal for ordinal, continuous, or skewed data distributions
c) Mode can be applied to both numerical and categorical data
5) Uniqueness:
a) Mean is always a single, unique value for a dataset
b) Median is a single value, except when the dataset is even, in which case it is the average of the two middle values.
c) Mode may not exist if no value repeats, and it can have multiple values if several values share the highest frequency.
Conclusion
Grasping Mean Median Mode transforms raw data into meaningful stories. These statistical tools are your secret weapons for decoding everything from academic results to business metrics. By mastering them, you gain the ability to see beyond the numbers and make smarter, data-driven decisions.
Your journey into data begins here with our Statistics Course - Sign up today!
Frequently Asked Questions

The Mean, Median, and Mode Rule describes central tendencies in data:
a) Mean: Average of all values
b) Median: Middle value when data is sorted
c) Mode: Most frequently occurring value

The Mean, Median, and Mode Formula:
a) Mean:
Mean = Sum of All Values / Number of Values
b) Median:
Median = Middle Two Values Sum / 2
c) Mode:
The value that occurs most frequently in the data set

The Knowledge Academy takes global learning to new heights, offering over 30,000 online courses across 490+ locations in 220 countries. This expansive reach ensures accessibility and convenience for learners worldwide.
Alongside our diverse Online Course Catalogue, encompassing 19 major categories, we go the extra mile by providing a plethora of free educational Online Resources like News updates, Blogs, videos, webinars, and interview questions. Tailoring learning experiences further, professionals can maximise value with customisable Course Bundles of TKA.

The Knowledge Academy’s Knowledge Pass, a prepaid voucher, adds another layer of flexibility, allowing course bookings over a 12-month period. Join us on a journey where education knows no bounds.

The Knowledge Academy offers various Business Analyst Courses, including the Statistics Course, Statistical Process Control Training and the Mathematical Optimisation for Business Problems. These courses cater to different skill levels, providing comprehensive insights into Inferential Statistics.
Our Business Analysis Blogs cover a range of topics related to Statistics and Math Operations, offering valuable resources, best practices, and industry insights. Whether you are a beginner or looking to advance your Statistical Skills, The Knowledge Academy's diverse courses and informative blogs have got you covered.
Upcoming Business Analysis Resources Batches & Dates
Date
 Statistics Course
Statistics Course
Fri 21st Feb 2025
Fri 25th Apr 2025
Fri 20th Jun 2025
Fri 22nd Aug 2025
Fri 17th Oct 2025
Fri 19th Dec 2025







 Top Rated Course
Top Rated Course



 If you wish to make any changes to your course, please
If you wish to make any changes to your course, please


