We may not have the course you’re looking for. If you enquire or give us a call on 01344203999 and speak to our training experts, we may still be able to help with your training requirements.
We ensure quality, budget-alignment, and timely delivery by our expert instructors.

If you had to rank the most ubiquitous shapes in existence, the cylinder would be among the top tiers. From soda cans and water bottles to fire extinguishers, this shape not only plays an integral role in our daily lives but is also a fundamental shape in many fields, including engineering. This blog dissects one key aspect—the Surface Area of a Cylinder, which measures the total area that the surface of a cylindrical object occupies. So read on, master the mathematics behind Cylinders and deepen your appreciation for this important shape!
Table of Contents
1) What is the Surface Area of a Cylinder?
2) How to Calculate the Surface Area of Cylinder?
3) Formula for Surface Area of a Cylinder
4) Steps to Calculate the Surface Area of a Cylinder
5) Total Surface Area of Cylinder (TSA)
6) Practical Examples of Cylinder Surface Area Calculation
7) What is the Cross-sectional Area of a Cylinder?
8) What is the Difference Between Surface Area and Cross-sectional Area?
9) Conclusion
What is the Surface Area of a Cylinder?
A Cylinder is a 3D figure with two circular bases that are parallel and connected by a curved surface. It can be visualised as a series of stacked circles, all identical in size, arranged in a straight line. The Surface Area of a Cylinder refers to the area covering the outer surface of the cylinder. To calculate the total surface area, you must find the area of the three parts of its surface and add them together. Understanding the volume of a cylinder can also help in visualizing the relationship between the internal and external measurements of the cylinder.
How to Calculate the Surface Area of Cylinder?
Here are the steps to calculate a cylinder’s surface area:
1) Identify the radius of the cylinder
2) Identify the height of the cylinder
3) Calculate the area of the circular bases
4) Calculate the lateral surface area
5) Add the areas together
The process of calculating the surface is explored in detail below:
Formula for Surface Area of a Cylinder
The Surface Area of a Cylinder is the total area covered by its two circular bases and the curved surface that wraps around them. The formula for calculating the Surface Area of a Cylinder is given by:
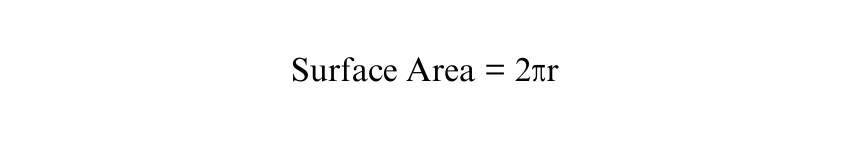
Where:
r = radius of the circular base.
h = the height of the Cylinder.
π is a constant approximately equal to 3.14159.
This formula combines the areas of the two circular bases
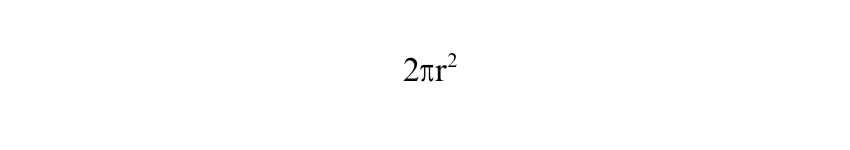
and the curved surface area 2πrh

Steps to Calculate the Surface Area of a Cylinder
Calculating the Surface Area of a Cylinder involves a few straightforward steps:
1) Measure the Radius and Height: Start by measuring the radius of the base (r) and the height (h) of the Cylinder.
2) Apply the Formula: Plug the values of r and h into the surface area formula: 2πr (h + r).
3) Calculate: Perform the calculations by multiplying and adding as per the formula. Don't forget to square the radius where necessary and multiply by π.
4) Interpret the Results: The result will give you the surface area in square units (e.g., square centimetres, square metres).
Take the leap! Equip yourself with the latest engineering skills and stand out in the job market. Register for our Engineering Skills Training today!
Total Surface Area of Cylinder (TSA)
Before we dive into the total Surface Area of a Cylinder, it’s important to consider the following points:
1) The curved Surface Area of a Cylinder is a rectangle
2) The circumference of the circle is the rectangle's length
3) The height of the Cylinder is the rectangle's height
So, the total surface area will be the sum of the area of the two circles and the curved surface area.
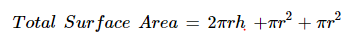
Where
r = Radius of the circle
h = Height of the Cylinder
2πrh = Curved surface area
πr2 = Area of the circle
Practical Examples of Cylinder Surface Area Calculation
Let’s explore some practical examples to solidify our understanding of how to calculate the Surface Area of a Cylinder.
Example 1: Calculating the Curved Surface Area
Suppose you have a Cylinder whose radius is 3 cm and height is 7 cm. The first step is to calculate the curved surface area, which is given by the formula:

Substitute the given values:
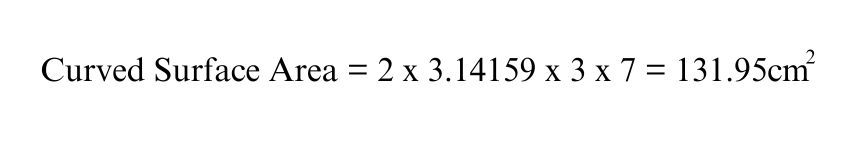
So, the curved surface area is 131.95 square centimetres
Example 2: Curved Surface Area Expressed in Terms of π
For a more general form, suppose the Cylinder's radius is 5 units, and the height is 10 units. The curved surface area can be expressed in terms of π:
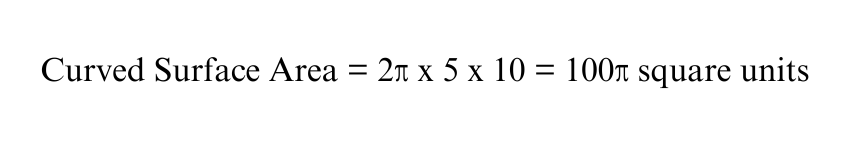
Here, the surface area is left in terms of π, making it more convenient for further mathematical operations.
Example 3: Finding the Total Surface Area
Now, let’s find the total surface area of a Cylinder where the radius is 4 cm, and the height is 9 cm. Using the surface area formula:
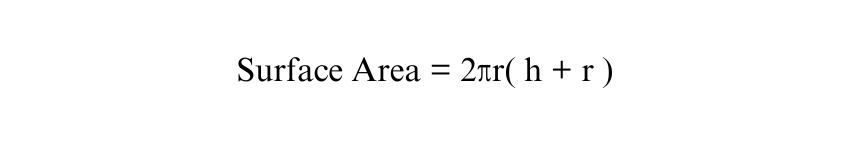
Substitute the values:
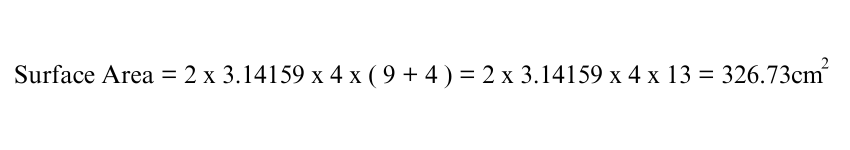
Thus, the total surface area is 326.73 square centimetres.
Become the best version of you! Unlock your potential with our Personal Development Training and start your transformation today!
What is the Cross-sectional Area of a Cylinder?
The cross-sectional area of a Cylinder generally refers to the circular shape as seen from top.
What is the Difference Between Surface Area and Cross-sectional Area?
Area is the space used by an object when it is resting on a surface. Meanwhile, a cross-section is obtained when the same object is cut into two pieces. The area of that cross-section is known as the cross-sectional area.
Conclusion
Understanding how to calculate the Surface Area of a Cylinder, as well as the Volume of a Sphere, is an essential skill in geometry. Whether you're working with physical objects or solving theoretical problems, the ability to determine both the surface area and volume can be highly beneficial. The formulas and calculations outlined in this blog will help you tackle any technical challenges related to Cylinders and the Volume of a Sphere.
Shape your future today. Our Career Development Course is the boost you need; register now and take charge of your career path!
Frequently Asked Questions
What is an Example of a Cross-sectional Area?

A Cylinder-shaped object cut by a plane that is parallel to the base will reveal a circle. This circle is an example of a cross-sectional area.
What is the Ratio of Curved Surface Area of Cylinder and Surface Area of Sphere?

If the Cylinder encloses the sphere, the Cylinder's radius will be equal to the sphere's radius, and the Cylinder's height will be equal to the sphere's diameter.
Radius = r
Cylinder height (h) = Sphere's diameter (2r)
Thus, h = 2r
The sphere's surface area = 4πr2
Cylinder's curved surface = 2πrh =2πr x 2r = 4πr2
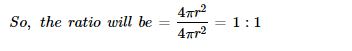
What are the Other Resources and Offers Provided by The Knowledge Academy?

The Knowledge Academy takes global learning to new heights, offering over 3,000 online courses across 490+ locations in 190+ countries. This expansive reach ensures accessibility and convenience for learners worldwide.
Alongside our diverse Online Course Catalogue, encompassing 19 major categories, we go the extra mile by providing a plethora of free educational Online Resources like News updates, Blogs, videos, webinars, and interview questions. Tailoring learning experiences further, professionals can maximise value with customisable Course Bundles of TKA.
What is The Knowledge Pass, and How Does it Work?

The Knowledge Academy’s Knowledge Pass, a prepaid voucher, adds another layer of flexibility, allowing course bookings over a 12-month period. Join us on a journey where education knows no bounds.
What are the Related Courses and Blogs Provided by The Knowledge Academy?

The Knowledge Academy offers various Personal Development Courses, including the Engineering Skills Training, Time Management Training and the Supervisor training. These courses cater to different skill levels, providing comprehensive insights into Best Courses After 12th.
Our Business Skills Blogs cover a range of topics related to Engineering, offering valuable resources, best practices, and industry insights. Whether you are a beginner or looking to advance your Engineering skills, The Knowledge Academy's diverse courses and informative blogs have got you covered.
Upcoming Business Skills Resources Batches & Dates
Date
 Engineering Skills Training
Engineering Skills Training
Fri 16th May 2025
Fri 18th Jul 2025
Fri 19th Sep 2025
Fri 21st Nov 2025






 Top Rated Course
Top Rated Course



 If you wish to make any changes to your course, please
If you wish to make any changes to your course, please


