We may not have the course you’re looking for. If you enquire or give us a call on +1 6474932992 and speak to our training experts, we may still be able to help with your training requirements.
Training Outcomes Within Your Budget!
We ensure quality, budget-alignment, and timely delivery by our expert instructors.

When you hear the word “pyramid,” your mind might wander to the majestic Great Pyramid of Giza. However, mastering the Volume of a Square Based Pyramid is a modern-day skill that goes beyond ancient wonders. In this blog, we’ll simplify the steps and formulas, making it easy for you to solve any pyramid-related problem with confidence.
We’ll break down the process into manageable parts, ensuring you understand each step clearly. Whether you’re a student tackling geometry homework or just someone curious about mathematical concepts, this blog on Volume of a Square Based Pyramid will equip you with the knowledge you need. So, let’s dive in and conquer those pyramid puzzles together!
Table of Contents
1) The Formula for the Volume of a Square Based Pyramid
2) How to Calculate the Volume of a Square Based Pyramid
3) Examples of Square Based Pyramid Volume Calculations
a) Calculating the Volume with a Given Height
b) Determining the Volume with a Known Height
c) Finding the Volume without the Perpendicular Height
d) Computing the Volume without Given Perpendicular Height
e) Determining the Height Given the Volume
f) Calculating the Base Length Given the Volume
4) Conclusion
The Formula for the Volume of a Square Based Pyramid
The Volume of a Square Based Pyramid represents the three-dimensional space enclosed by the pyramid's surfaces. The general formula is:
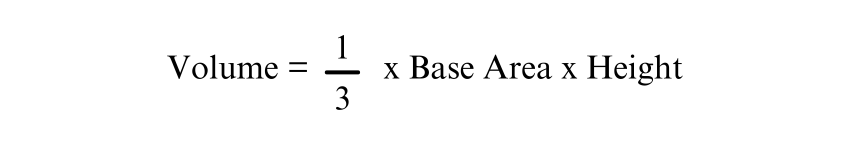
For a square based pyramid, the base is a square, so the area of the base can be calculated by squaring the length of one of its sides:
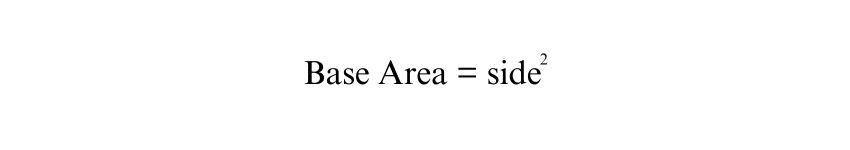
This formula indicates that the area of the base is simply the square of the length of one side of the square. When you know the side length of the base and the Height of the pyramid (which is the perpendicular distance from the base to the apex), you can substitute these values into the formula to find the volume:
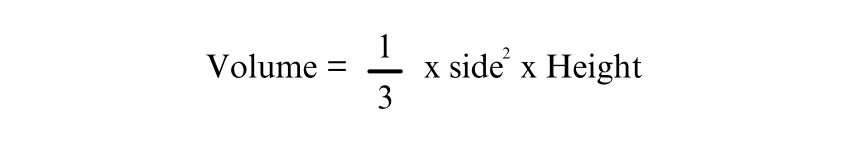
This formula is essential because it provides a direct method for calculating the Volume of a Square Based Pyramid, which is commonly encountered in various fields such as architecture, engineering, and mathematics. By understanding and applying this formula, you can determine the volume of any square based pyramid if you know its base's side length and Height. This foundational formula is used across different contexts, from academic exercises to real-world applications, making it a crucial tool in geometric calculations.
How to Calculate the Volume of a Square Based Pyramid?
Calculating the Volume of a Square Based Pyramid involves several straightforward steps:
1) Measure the Side Length of the Base: Start by measuring the length of one side of the square base. Ensure that the measurement is the same unit as the Height.
2) Square the Side Length to Find the Base Area: Multiply the side length by itself to determine the area of the square base:
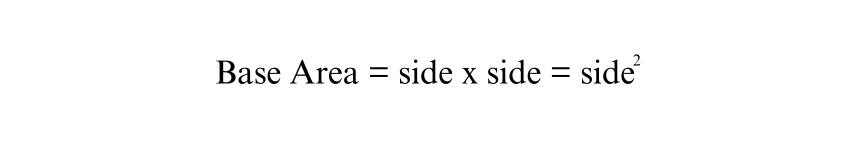
3) Measure the Height of the Pyramid: Measure the perpendicular Height from base to apex.
4) Apply the Formula to Find the Volume: Insert the base area and Height into the volume formula:

5) Calculate the Volume: Perform the multiplication to find the volume of the Pyramid in cubic units.
Improve your communication skills with our Active Listening Training. Sign up now!
Examples of Square Based Pyramid Volume Calculations
Let’s dive into some examples to solidify your understanding of calculating the Volume of a Square Based Pyramid.
1) Calculating the Volume with a Given Height
Example:
Suppose you have a Square Based pyramid with a side length of 6 metres and a height of 10 metres. The volume is calculated as follows:
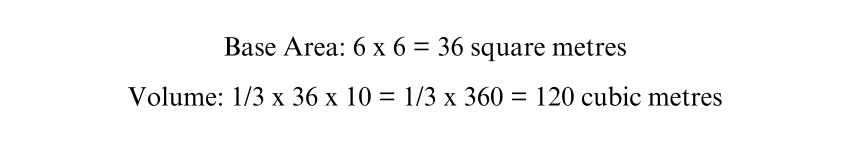
2) Determining the Volume with a Known Height
Example:
For a pyramid with a base side length of 4 cm and a height of 9 cm, the calculation is:
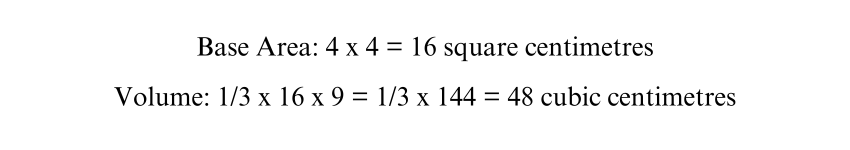
Need help calculating the Volume of a Cone? Explore our easy-to-follow guide and master the formula with real-life examples!
3) Finding the Volume without the Perpendicular Height
In some cases, the perpendicular Height might not be directly given, and you might need to derive it using other known values, such as the slant height and the Pythagorean theorem.
Example:
Given a slant height of 10 metres and a base side length of 8 metres, the perpendicular Height can be calculated using:
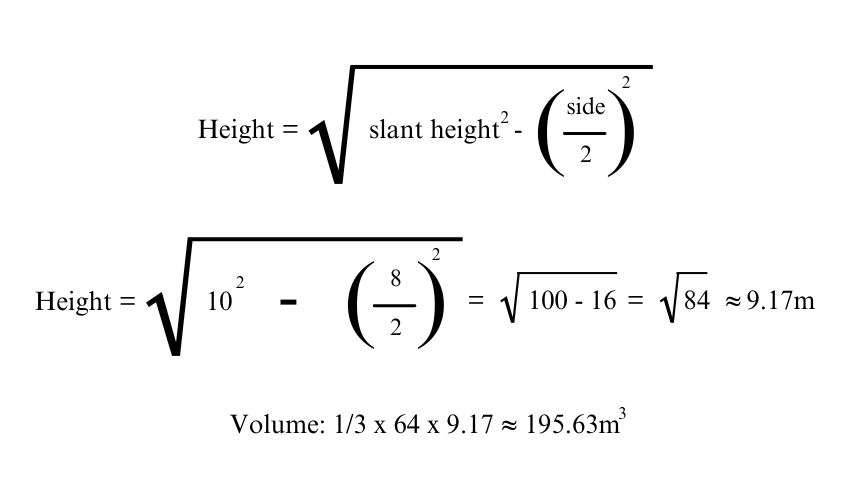
4) Computing the Volume without Given Perpendicular Height
If you have the slant height but not the perpendicular Height, you can still find the volume by first determining the Height using trigonometric relationships or the Pythagorean theorem.
Example:
Given a base side length of 8 metres and a slant height of 10 metres, find the perpendicular Height:
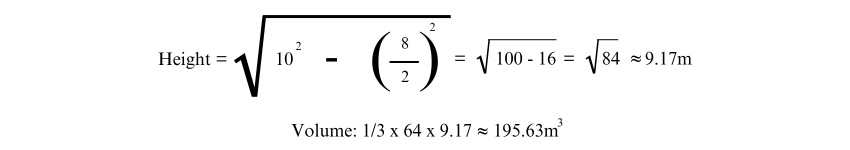
5) Determining the Height Given the Volume
If you know the volume and the base side length, you can determine the Height of the pyramid by rearranging the volume formula:
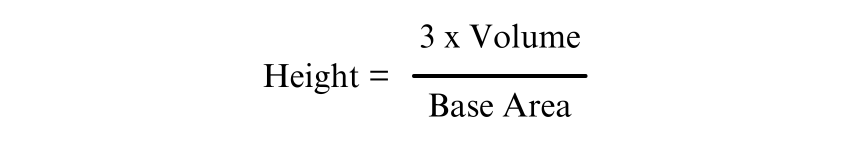
Example:
For a pyramid with a volume of 75 cubic metres and a base side length of 5 metres:
6) Calculating the Base Length Given the Volume
If the volume and height are known, you can find the base length by rearranging the formula to solve for the side length:
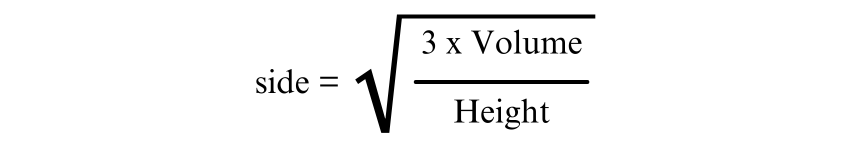
Example:
Given a volume of 81 cubic metres and a height of 9 metres:
Maximise your efficiency with our Time Management Training. Sign up now!
Conclusion
Understanding the Volume of a Square Based Pyramid is not just about memorising formulas—it’s about grasping the underlying concepts and applying them with confidence. By breaking down the steps and simplifying the process, we’ve made it easier for you to tackle any pyramid-related problem that comes your way. Whether you’re a student, a teacher, or simply a math enthusiast, this knowledge empowers you to approach geometry with a newfound clarity.
Boost your productivity with our Speed Writing Course – Join now!
Frequently Asked Questions

The formula is volume= 1/3 x Base Area x Height, where the base area is calculated as Side².

Yes, if you have the slant height and the base side length, you can use the Pythagorean theorem to find the perpendicular Height, which allows you to calculate the volume.

The Knowledge Academy takes global learning to new heights, offering over 30,000 online courses across 490+ locations in 220 countries. This expansive reach ensures accessibility and convenience for learners worldwide.
Alongside our diverse Online Course Catalogue, encompassing 19 major categories, we go the extra mile by providing a plethora of free educational Online Resources like News updates, Blogs, videos, webinars, and interview questions. Tailoring learning experiences further, professionals can maximise value with customisable Course Bundles of TKA.

The Knowledge Academy’s Knowledge Pass, a prepaid voucher, adds another layer of flexibility, allowing course bookings over a 12-month period. Join us on a journey where education knows no bounds.

The Knowledge Academy offers various Personal Development Courses, including Engineering Skills Training, Time Management Training and Active Listening Training. These courses cater to different skill levels and provide comprehensive insights into the Area of a Circle
Our Business Skills blogs cover a range of topics related to Personal Development, offering valuable resources, best practices, and industry insights. Whether you are a beginner or looking to advance your Engineering Skills, The Knowledge Academy's diverse courses and informative blogs have got you covered.
Upcoming Business Skills Resources Batches & Dates
Date
 Engineering Skills Training
Engineering Skills Training
Fri 17th Jan 2025
Fri 21st Feb 2025
Fri 4th Apr 2025
Fri 6th Jun 2025
Fri 25th Jul 2025
Fri 7th Nov 2025
Fri 26th Dec 2025







 Top Rated Course
Top Rated Course



 If you wish to make any changes to your course, please
If you wish to make any changes to your course, please


