Six Sigma Control Charts: All you Need to Know

Six Sigma Control Charts are essential tools within the Six Sigma methodology. They monitor and analyse process variations. Business enterprises can identify and address process deviations by plotting data points against control limits leading to improved quality, reduced defects, and enhanced overall performance.  

Furthermore, the Control Chart visually represents the business process performance and helps identify common causes and variations. Read this blog to learn about the Six Sigma Control Charts, their types, how to create and plot charts, interpreting them and more. 

Table of Contents 

1) What is Six Sigma Control Chart? 

2) Working of Six sigma Control Charts   

3) Types of Six Sigma Control Charts 

4) 3 elements of Six Sigma Control Chart

5) Creating and plotting control charts 

6) How to calculate Control Limits

7) How do you interpret a Six Sigma Control Chart?

8) When to use Sigma Six chart 

9) Conclusion

What is Six Sigma Control Chart? 

The Six Sigma Control Chart is vital to the Six Sigma methodology. It aims at achieving process stability and enhancing overall quality. It provides businesses with a visual representation of process variation, so they can monitor and analyse data, identify patterns, and make data-driven decisions for continuous improvement.  

What is a Control Chart in Six Sigma? Well, it is a graphical tool that helps organisations understand the nature of process variation. It shows data points in a time series or a sequence, with a centreline indicating the process average and upper and lower limits representing acceptable variation.  

Furthermore, Control Charts differentiate between the common cause and special cause variation. Common cause variation refers to the normal, inherent fluctuations within a process, while special cause variations indicate factors outside the usual process conditions.  

Moreover, several Control Charts are commonly used in Six Sigma, including the X-bar and R chart, the X-bar and S chart, and the individual chart. The X-bar charts monitor a process's average or mean value, while the R and S charts track the variability or range within the process.  

Businesses must follow a systematic approach to utilise Control Charts effectively. This begins with accurate and representative data collection. A robust data collection plan ensures that the right data points are selected appropriately, allowing for a comprehensive understanding of process performance.  

Plotting the Control Chart involves charting the collected data points and control limits. This visual representation enables easy identification of patterns, trends, shifts, or outliers. Additionally, it provides a holistic view of process performance, making it easier to detect deviations and take appropriate corrective actions.

 

Working of Six sigma Control Charts  

Control Charts are graphical tools that help you assess the stability of a process. They plot the output of the process over time and show the patterns of variation. If the result of a process deviates too much from the expected range, it means that the process is unstable and needs to be improved.

A Control Chart is also known as a Stewart Chart, after its inventor William A. Stewart in 1926. The process behaviour is also called a behaviour chart, which reflects how the process changes over time. However, in the Six Sigma study, Control Charts are usually used in the control phrases.

Working of Six Sigma Control Charts involves monitoring and analysing process data to ensure that process remains stable and predictable. Here are some pointers: 

Data collection

Initially, you need to collect data from the process you are monitoring. This data could be measurements, observations, or any relevant metrics that reflect the performance of the process.   

Calculate central line and control limits

Based on the collected data, calculate the central line and control limits. The central line represents the average performance of the process, and the control limits define the acceptable range of variation around the central line. Control limits are usually calculated through statistical methods.  

Plotting data points

Plot the collected data points on the Control Chart. The horizontal axis represents time or the sequence of data collection, while the vertical axis represents the measured value. Also include elements central line, Upper control limit, and limit control limit on the chart.  

Interpretation and analysis

After plotting data points, observe their behaviour in relation to cental line and control limits. Here are few key patterns to look for:

a) Within control limits: If the data points cluster around central line, it means the process is stable and predictable.

b) Points outside control limits: If the data points fall outside the control limits, it suggests a special cause of variation which leads to process deviations. It's important to investigate and address the issue causing deviation.

Action and improvement

When points tend to fall outside the control limits or patterns, it becomes imperative  to take action, investigate the root causes of deviations and implement the right actions. The goal is to bring the process back into control and reduce variability.

Continuous monitoring

The process of collecting data, updating chart, and taking corrective actions is ongoing. Regular monitoring helps ensure the process remains stable and produces high-quality results. 

Types of Six Sigma Control Charts 

Six Sigma utilises different Control Charts to monitor and analyse process variation, enabling organisations to identify and address deviations effectively. Here are the main types of control charts commonly used:  

a) X-bar and R Chart: This chart tracks the process mean (X-bar) and the range (R) within subgroups. It helps monitor the average performance and variability of a process over time. The X-bar chart helps identify shifts or trends in the process mean, while the R chart provides insights into the process variability.

This Control Chart allows businesses to assess process stability, detect outliers, and make informed decisions for process improvement by plotting subgroup averages and ranges over time. It is particularly useful when dealing with continuous data and stable subgroup sizes.   

b) X-bar and S Chart: Like the X-bar and R chart, this control chart monitors the process mean (X-bar) and the standard deviation (S) within subgroups. It is used when the range may not be an appropriate measure of variability. This chart is helpful when the range is not a proper measure of variability or when the subgroup size varies.

Furthermore, it enables businesses to evaluate process stability, identify shifts or trends in the process mean, and understand variations in process variability. The X-bar and S chart complements the X-bar and R chart and provides valuable insights for process improvement efforts.  

c) Individuals Chart: This Control Chart tracks individual data points rather than subgroup averages. It is suitable for processes where subgroups are impractical or unnecessary. It is particularly useful when subgroups are impractical to form or when the process is naturally performed.

The chart consists of individual data points plotted over time, along with control limits based on the range of the data. The Individuals chart helps identify process variation, detect special cause variation, and monitor process stability. It allows businesses to observe the performance of individual data points, identify outliers, and take appropriate actions for process improvement and quality control.  

The above charts have advantages and are selected based on the analysis of specific process features. These Control Charts provide valuable insights into process performance, facilitating data-driven decision-making and continuous improvement efforts in Six Sigma projects. 

Learn the fundamentals of Six Sigma methodology by signing up for the Six Sigma Yellow Belt Course now! 

Choosing the right Control Chart

Selecting the appropriate Six Sigma Control Chart is crucial for accurate analysis and effective process improvement. Different control charts are designed to monitor specific aspects of process variation, and choosing the right one depends on various factors. Here are some considerations to keep in mind when selecting a control chart: 

a) Type of data: Consider the type of data being collected. If the data is continuous and normally distributed, X-bar and R Charts or X-bar and S Charts are suitable. Alternative control charts like the Individuals chart or the C (count) chart may be more appropriate for discrete data or non-normal distributions.  

b) Subgroup size: Evaluate the size of the subgroups being analysed. X-bar and R Charts and X-bar and S Charts are typically used when subgroup sizes are relatively small and consistent. If the subgroup sizes vary or are impractical to form, the Individuals chart can be employed to monitor individual data points.  

c) Measurement scale: Determine the measurement scale of the data. Control Charts like the X-bar and R Charts are suitable for variable data involving continuous measurements. Attribute data, which represents the presence or absence of a specific characteristic, can be monitored using control charts such as the P (proportion) chart or the C chart.  

d) Purpose of analysis: Consider the specific objectives of the analysis. Different Control Charts provide insights into different aspects of process variation. X-bar Charts are effective for monitoring process central tendency, while R and S Charts assess process variability. Attribute Control Charts are used to monitor the proportion or count of nonconforming items.  

e) Stability of process: Assess the stability of the process being monitored. Traditional Control Charts can be employed if the process is stable and in control. However, if the process exhibits significant variability or special cause variation, advanced Control Charts like the Multivariate Control Chart or the Time-weighted control chart may be necessary. 

Assist with data collection and analysis by signing up for the Six Sigma Green Belt Training Course now! 

3 elements of Six Sigma Control Chart
 

The Six Sigma Control Chart helps in monitoring and analysing the stability and performance of a process over time. There are three essential elements of Six Sigma Control Chart which are: 

Data points

These are the actual measurements or observations collected from the process over time. These data points represent the performance of the process at specific intervals. It represents the actual output of the process over time.  

Central line 

The central line on a Control Chart represents the mean or process average. It's often represented by a horizontal line and is calculated based on the historical data points collected. This line provides a reference point which helps in understanding whether the process is centred around the desired target or goal.

Control limits

Control limits are the upper and lower boundaries on the Control Chart that define the acceptable variation in the process. There are usually two sets of control limits: Upper Control Limit (UCL) and Lower Control Limit (LCL). These limits are calculated based on statistical principles and the inherent variability of the process.

Creating and plotting Control Charts 

Creating and plotting a Six Sigma Control Chart involves careful data collection and establishing control limits. Accurate and representative data must be collected following a well-defined plan. Control limits are calculated using statistical measures such as mean, range, or standard deviation.   

Once the data and control limits are ready, the Control Chart is plotted, visually representing the process performance. This graphical representation helps identify patterns, trends, or shifts, enabling businesses to take appropriate corrective actions for process improvement. Following are the three aspects of creating and plotting control charts: 

a) Data collection and preparation: This involves gathering data and ensuring its accuracy and representativeness for Control Chart analysis. It requires defining a data collection plan, selecting appropriate data points, and ensuring consistency and reliability in data collection methods. Careful preparation is crucial to ensuring the validity and relevance of the data used in Control Chart analysis. 

b) Calculating Control limits: Control limits are statistical boundaries that determine an acceptable variation within a process. They are calculated using mean, range, or standard deviation measures. These calculations provide benchmarks for evaluating process stability and identifying deviations from the desired performance. Accurate control limits are essential for effective Control Chart analysis and interpretation.  

c) Plotting Control charts: Once the data and control limits are determined, Control Charts are created by plotting the data points against the control limits. This graphical representation allows for visual analysis of process performance. Control chart patterns, including shifts, trends, or outliers, can be easily identified, enabling businesses to make data-driven decisions and take appropriate corrective actions for process improvement. 

Gain business improvement insight by signing up for the Six Sigma Black Belt Course now!  

How to calculate control limits?

The 3-Sigma method is a widely used approach to calculate control limits in a Six Sigma Control Chart. It involves using the standard deviation of collected data. It begins with finding the average and standard deviation of collected data. This average serves as the centreline, while the standard deviation measures data dispersion around it. 

Control limits are determined using a Z-score, showing desired control level (for example, 3 for high control). The UCL is found by adding Z-score times standard deviation to the average, and the LCL is obtained by subtracting the same product. 

Data points within UCL and LCL indicate normal variations; those beyond signal special causes need investigation. This approach helps maintain process stability, detecting deviations and enabling corrective actions to ensure quality and performance.

Determine the correct strategy for your projects by signing up for the Six Sigma Master Black Belt Course now!

How do you interpret a Six Sigma Control Chart?

Interpreting a Six Sigma Control Chart involves analysing the data points on the chart in relation to the central line and control limits. Here are some pointers on how to interpret a Six Sigma Control Chart:

Centreline

Centreline represents the average of the process data. If the data points cluster around this line, it indicates that the process is performing close to its target. If most data points are on or near the central line, the process is stable and predictable.

Control limits

The UCL and LCL are set based on statistical calculations, which involve the standard deviation. Data points within these limits show normal variation.

Within control limits

Data points falling between the UCL and LCL indicate variation-normal fluctuations due to inherent process variability.

Outside control limits

Data points beyond the control limits suggest special cause variations, which results in unusual occurrences.

Immediate action

When a data point falls outside the control limits, consider investigating the cause and taking corrective measures.

When to use Sigma Six Chart
 

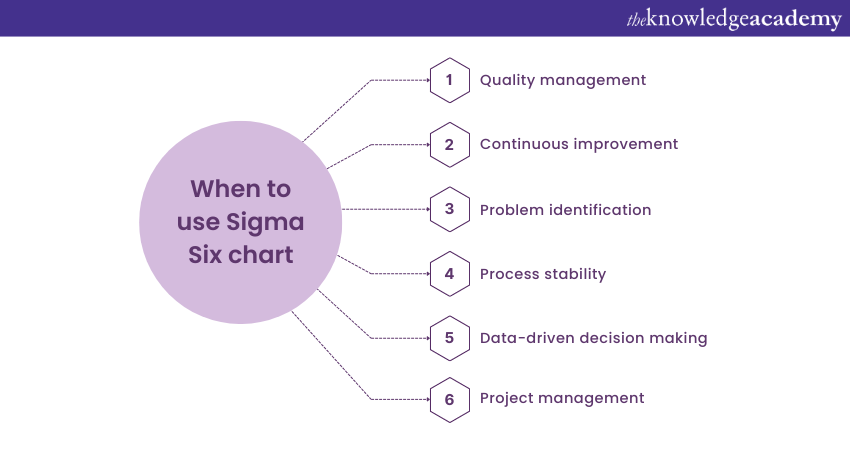
Sigma Six Chart is used in situations where maintaining high process quality and minimising defects are important. Here are some instances when to use a Sigma Six Chart:

Quality management

Monitor the quality of a manufacturing or service process; a Control Chart helps in identifying variations that might lead to defects or errors.

Continuous improvement

It emphasises continual process improvement. Using Control Charts, you can track whether your improvements are effective in reducing variation.

Problem identification

Control Charts help quickly identify issues by flagging data points that fall outside control limits.

Process stability

Control Charts provide a clear visual representation of the stability of your process over time.

Data-driven decision making

Control Charts excel at differentiating between common cause and special cause variation.

Project management

It involves analysing trends and patterns on Control Charts charts; you can make informed decisions about process adjustments and improvements based on real data.  

Ready to become a process improvement champion? Register for our Six Sigma Black Belt Upgrade Course to master the art of data-driven decision making. 

Conclusion 

Selecting the right Six Sigma Control Chart is critical to conducting effective process analysis and improvement. Businesses can make informed decisions by considering the type of data, subgroup size, measurement scale, analysis objectives, and process stability. Choosing the appropriate Control Chart allows for accurate monitoring of process variation, identification of improvement opportunities, and achieving enhanced quality and performance. 

Learn to eliminate defects through Business Improvement by signing up for Six Sigma Certification Training Courses now!