We may not have the course you’re looking for. If you enquire or give us a call on +352 8002-6867 and speak to our training experts, we may still be able to help with your training requirements.
Training Outcomes Within Your Budget!
We ensure quality, budget-alignment, and timely delivery by our expert instructors.

Imagine a shape that's partly rectangle and partly triangle with a unique twist—this is the Trapezium. Unlike regular shapes, a Trapezium has two parallel sides of different lengths. This makes its area calculation both fascinating and essential for various practical applications.
However, we cannot always find the Area of a Trapezium by drawing unit squares. It requires a standard mathematical formula. This standard formula would help us in this situation. Continue reading this exciting blog to delve into the details of the Area of a Trapezium and its formula for decoding it. Let’s get to the paradigm of mathematical fun!
Table of Contents
1) What is Trapezium?
2) Different Types of Trapeziums
3) Area of Trapezium Formula
4) Area of a Trapezium with a Parallelogram
5) Area of a Trapezium with a Triangle
6) Examples of the Area of a Trapezium
7) Conclusion
What is a Trapezium?
A Trapezium is a four-sided polygon that falls under the category of Quadrilaterals. It has only one set of parallel sides.
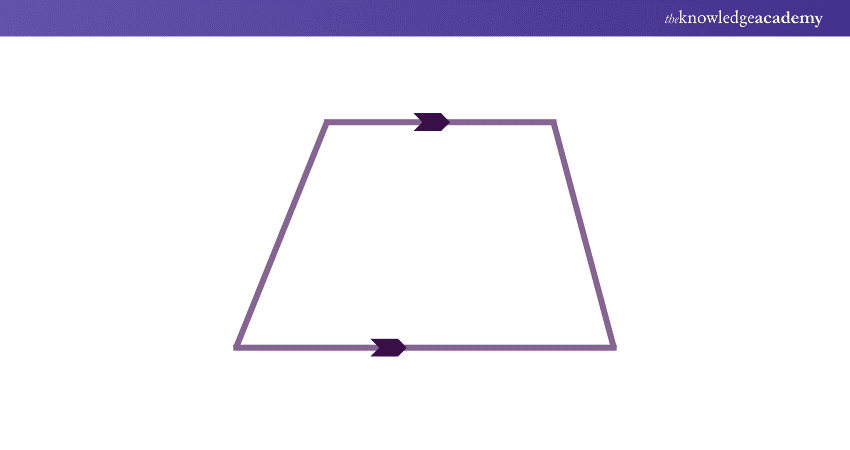
The Trapezium's area is the space inside its boundaries, measured in square units like cm², m², mm², etc.
Different Types of Trapeziums
Trapeziums can be categorised based on their characteristics described below. These include the lengths of their sides or the measurements of their angles.
1) Isosceles Trapezoid: An Isosceles Trapezoid has equal base angles, and its diagonals are the same length.
2) Scalene Trapezium: Scalene Trapezium has different base angles and diagonal lengths.
Area of Trapezium Formula
The area of a Trapezium can be calculated with the help of two parallel sides and the height of the Trapezium. The formula for calculating the area (A) of a Trapezium is:
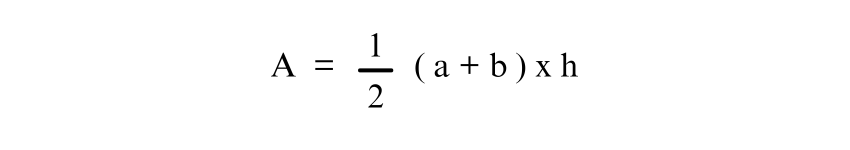
where:
'a and ‘b’ are the parallel sides’ lengths (bases),
'h’ is the perpendicular distance between the bases.
There are primarily two methods to derive this formula:
1) Using a Parallelogram: Rearranging two identical Trapeziums to form a Parallelogram’
2) Using a Triangle: Dividing the Trapezium into two Triangles and calculating their combined area.
Area of a Trapezium with a Parallelogram
Consider two identical Trapeziums with bases ‘a’ and ‘b’ and height ‘h’. Let us assume ‘A’ as the area of each Trapezium. Now, turn the second Trapezium upside down and attach it to the first one.
By joining the two Trapeziums, we can form a Parallelogram with an equal base of (a + b) and a height of ‘h’.
Thus,
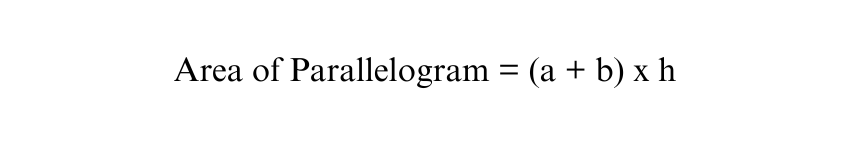
2) The area of the Parallelogram in terms of ‘A’ is the sum of the areas of the two Trapeziums:
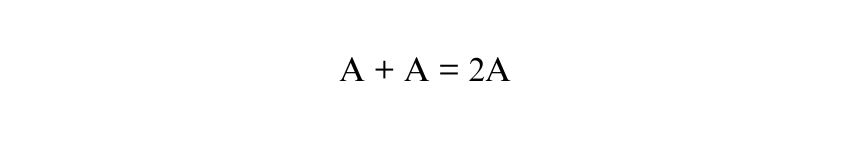
Therefore, the equation becomes:
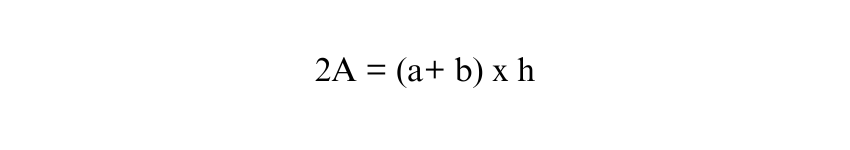
Learn the right techniques for prioritising tasks and increasing productivity with our Time Management Training – Register today!
Area of a Trapezium with a Triangle
To better understand how to derive the formula for the area of a Trapezium, let's explore a method using two identical Trapeziums. Follow these steps to get the formula for the area of a Trapezium:
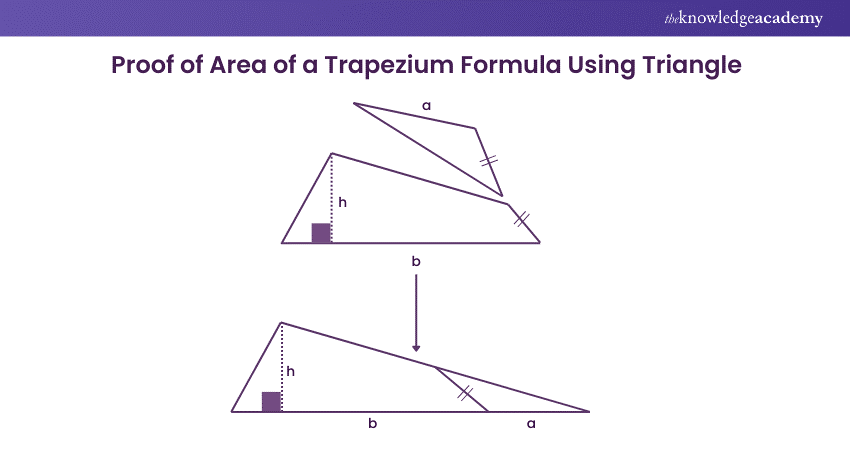
Step 1: Divide one of the non-parallel sides of the Trapezium into two equal parts.
Step 2: Cut out a triangular section from the Trapezium.
Step 3: Attach this triangular portion to the bottom of the shape.
Now, the Trapezium is rearranged to form a Triangle, and the areas of both shapes are identical. The base of the triangle is (a + b), while the height remains h.
Thus, the area of the Trapezium equals the area of the triangle, calculated as:
Area of Trapezium = Area of triangle = ½ × base × height = ½ (a + b) × h.
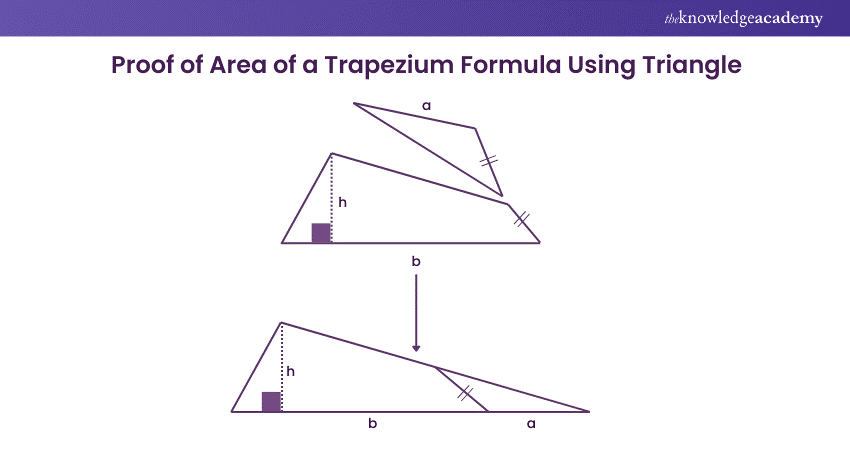
This rearrangement transforms the Trapezium into a triangle. From the diagram, it's clear that the areas of the original Trapezium and the newly formed triangle are the same. The triangle’s base is now equal to (a + b), and the height remains h.
Thus, the area of the Trapezium is the same as the area of the triangle, which can be calculated using the formula:
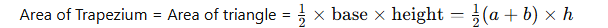
Learn cutting-edge strategic planning for business growth with our Strategic Planning and Thinking Course- Join now!
Examples of the Area of a Trapezium
To help clarify the process of calculating the area, let’s look at a few practical examples. Below we have illustrated different scenarios for calculating the area of a Trapezium.
Example 1: Determining the Area with Known Parallel Side Lengths and Height
If the lengths of the parallel sides are a = 8 units and b = 5 units, and the height h = 4 units, the area of the Trapezium can be calculated using the formula:
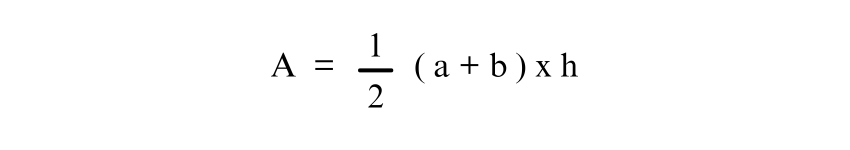
Substituting the given values:
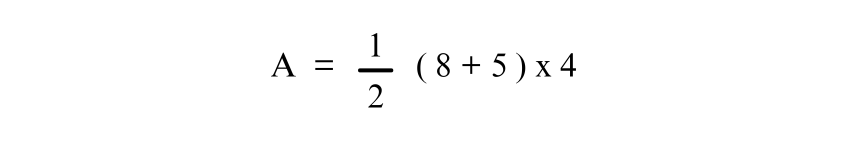
Simplifying
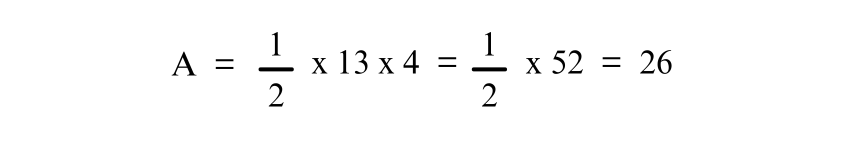
Thus, the area of the Trapezium is 26 square units.
Example 2: Finding the Area of a Trapezium with Unit Conversions
In this example, let’s say the parallel sides of the Trapezium are a = 500 cm and b = 300 cm, and the height is 2 meters. First, convert the height to centimetres:
Since 1 meter = 100 centimetres, we convert 2 meters to centimetres:
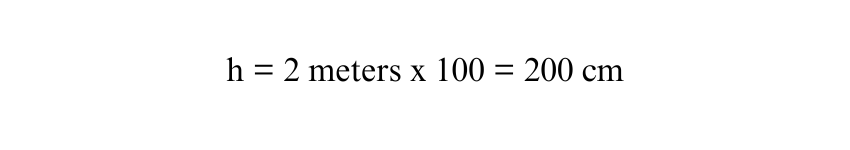
Now, using the formula for the area of the Trapezium:
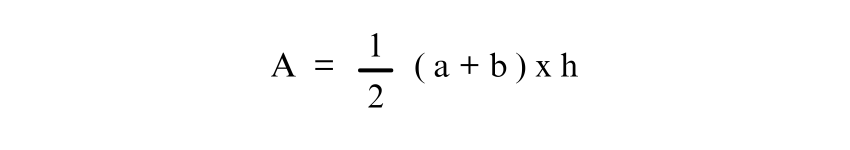
Substitute the known values:
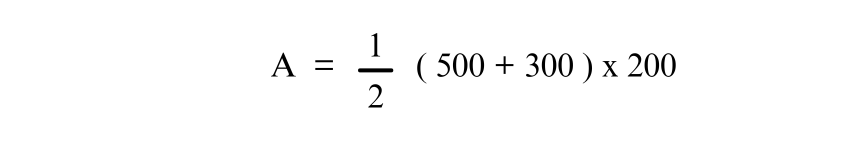
Simplifying:
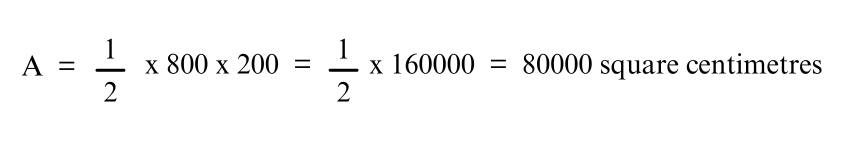
Thus, the area of the Trapezium is 80,000 square centimetres.
Example 3: Calculating the Height When the Area is Given
Suppose the area of the Trapezium is 45 square units, and the lengths of the parallel sides are a = 5 units and b = 3 units. To find the height h, use the formula and solve for h:
Substitute the known values in the Trapezium formula, we get:
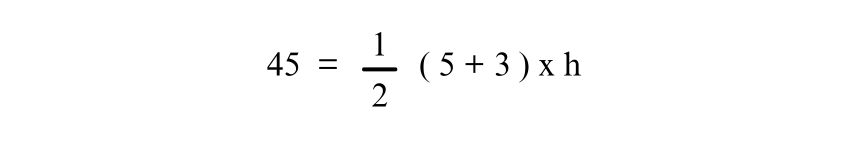
Simplifying the equation:
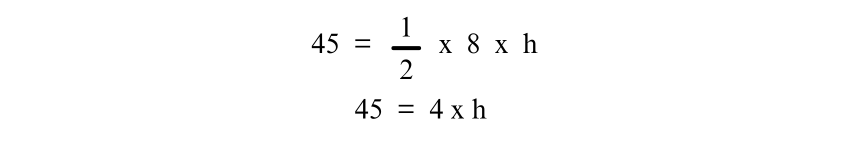
Now, solve for h by dividing both sides of the equation by 4:
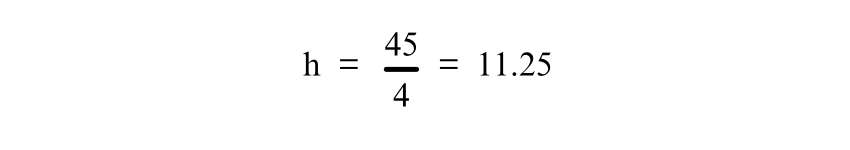
Thus, the height of the Trapezium is 11.25 units.
Example 4: Finding the Base Length When the Area is Known
If the area of the Trapezium is 64 square units, and the height is h = 4 units, with one of the parallel sides a = 10 units, find the other side b. Use the area formula and solve for b:
Substitute the known values into the Trapezium area’s formula:
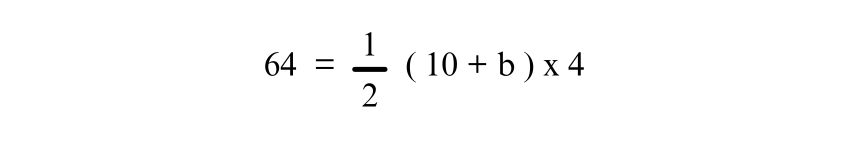
Simplifying the equation:
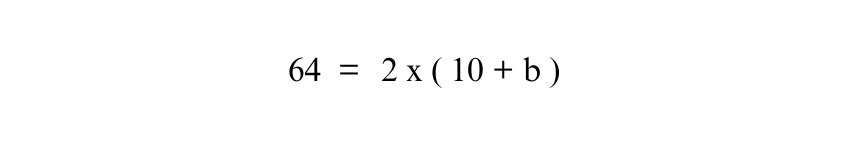
Now, divide both sides of equation by 2:
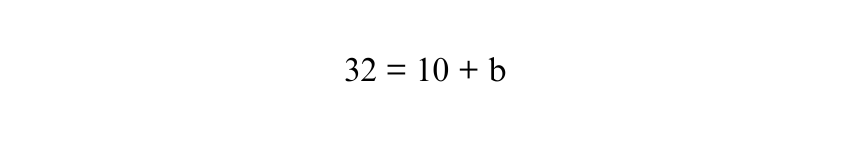
To find b, subtract 10 from both sides:
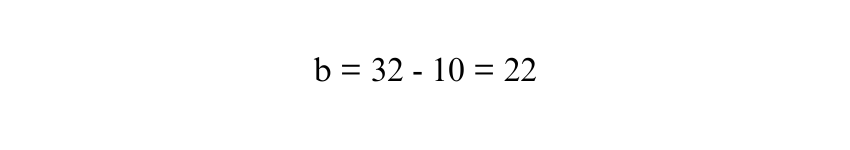
Thus, the length of the other parallel side b is 22 units.
What Is the Formula for the Height of a Trapezium Without Area?
To find the height of the Trapezoid, we must put all the other values into its area formula. This allows us to solve the problem of height when the area is not directly provided.
The basic formula for Trapezoid is
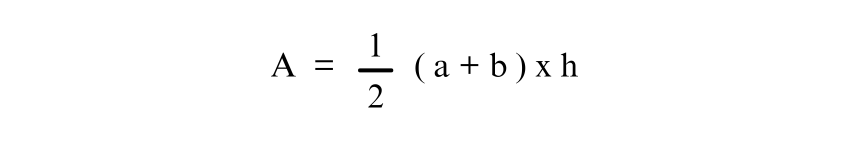
Where, a = long base
b= short base
h= height
Let’s suppose we have all other values besides height. Taking ‘h’ on one side, we multiply equation on both sides by 2 to eliminate the fraction,
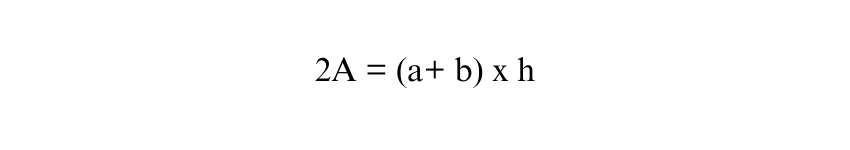
Now, solve for ’h’ by dividing both sides of the equation by (a+b)
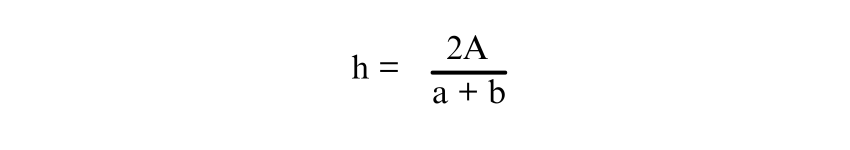
Thus, the formula for ‘h’ is
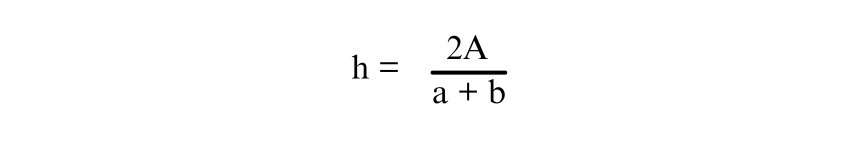
Learn proven stress reduction methods for success- join our Stress Management Course today!
Conclusion
The Area of a Trapezium can be easily calculated using the formula ½ × (a + b) × h. Here, ‘a’ and ‘b’ are the parallel side lengths, and ‘h’ is the height. This versatile formula makes solving geometric problems involving Trapeziums easy, whether you're working with the sides, height, or area.
Transform your financial strategies with the right budgets- sign up for our Introduction to Managing Budgets today!
Frequently Asked Questions

The rule for calculating the area of a Trapezium is ½ × (a + b) × h. Here, ‘a’ and ‘b’ are the lengths of the parallel sides, and ‘h’ is the height. This formula provides the space enclosed by the Trapezium based on its dimensions.

The Trapezium Theorem is also known as the Midsegment theorem. It states that the midsegment (the line connecting the middle points of the non-parallel sides) is parallel to the parallel sides and its length is the average of two parallel sides. This theorem is often used in geometry to understand Trapezium properties.

The Knowledge Academy takes global learning to new heights, offering over 30,000 online courses across 490+ locations in 220 countries. This expansive reach ensures accessibility and convenience for learners worldwide.
Alongside our diverse Online Course Catalogue, encompassing 19 major categories, we go the extra mile by providing a plethora of free educational Online Resources like News updates, Blogs, videos, webinars, and interview questions. Tailoring learning experiences further, professionals can maximise value with customisable Course Bundles of TKA.

The Knowledge Academy’s Knowledge Pass, a prepaid voucher, adds another layer of flexibility, allowing course bookings over a 12-month period. Join us on a journey where education knows no bounds.

The Knowledge Academy offers various Personal Development Courses, including Engineering Skills Training, Strategic Planning and Thinking Course, and Time Management Training. These courses cater to different skill levels, providing comprehensive insights into the Volume of a Sphere.
Our Business Skills Blogs cover a range of topics related to Personal Development, offering valuable resources, best practices, and industry insights. Whether you are a beginner or looking to advance your Business Skills, The Knowledge Academy's diverse courses and informative blogs have you covered.
Upcoming Business Skills Resources Batches & Dates
Date
 Engineering Skills Training
Engineering Skills Training
Fri 17th Jan 2025
Fri 21st Mar 2025
Fri 16th May 2025
Fri 18th Jul 2025
Fri 19th Sep 2025
Fri 21st Nov 2025







 Top Rated Course
Top Rated Course



 If you wish to make any changes to your course, please
If you wish to make any changes to your course, please


