Mean Median Mode: What They Are and How to Find

Statistics can sound intimidating, but what if we tell you, it all starts with three simple words: Mean Median Mode? They comprise a framework of approach to analysis of data; they assist in revealing patterns, in searching for the middle of information, and interpreting numbers in the real world. No matter if a learner, a worker, or someone who just wants to learn something about data, knowing these basics will be of big assistance.

In this blog, we will learn how to calculate the Mean Median Mode process one at a time. What you are to understand will include ungrouped and grouped data, applications, calculations, and differences. Read ahead to explore the world of data and get to know about how numbers speak for themselves.

Table of Contents

1) What is Mean Median and Mode in Statistics?

2) Steps to Calculate the Mean of a Data Set

3) Steps to Identify the Median

4) Steps to Find the Modal Value of a Data Set

5) Key Differences Between Mean, Median, and Mode

6) Solved Examples on Mean, Median and Mode

7) Summary of When to Use the Mean, Median and Mode

8) Conclusion

What is Mean Median and Mode in Statistics?

Mean, Median, and Mode are measures of central tendency in statistics. Mean is the average of all values, Median is the middle value in an ordered dataset, and Mode is the most frequently occurring value. They help summarise and interpret data effectively, especially in analysing distributions.

1) Mean

The Mean, often called the average, is calculated by adding all the values in a data set and dividing them by the number of values.

1) Ungrouped Data

For ungrouped data, the Mean is calculated as:

Mean = Sum of all values ÷ Number of values Sum of all values ÷Number of values

Example: If the values are 2,4,6,8,10 the Mean is:

Mean= 2+4+6+8+10 / 5 = 6

2) Grouped Data

For grouped data, the Mean is calculated by using the formula:

Mean = (Σ f * x) / (Σ f)

Where f is the frequency of a class interval and x is the midpoint

Where:

Example: If we have the following grouped data:

Class Interval	Frequency (f)	Midpoint (x)	f * x
0-10	4	5	20
10-20	6	15	90
20-30	10	25	250

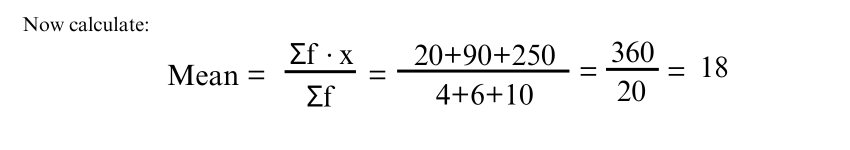
2) Median

The Median is the middle value that comes out when data is arranged in ascending order. It is a more robust measure when the data contains outliers.

1) Ungrouped Data

a) Arrange the data in order (ascending)

b) Odd Number of Values: The Median is the middle value

c) Even Number of Values: The Median is the Mean of the two middle values

Example: For 1,3,5,7,91, 3, 5, 7, 9 (odd):

Median = 5

For 1,3,5,7 (even): Median = 3+5 / 2 = 4

Transform your career with in-demand skills – join our Business Analyst Courses now!

2) Grouped Data

The formula for grouped data is:

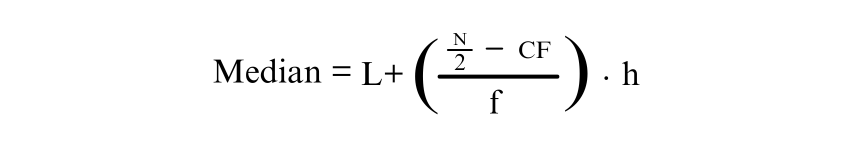
Where:

3) Mode

The Mode is the value that appears most frequently in a data set

1) Ungrouped Data

a) Identify the value(s) that occur most often

Example: For 2,2,3,4,4,4,5 the Mode = 4 (appears most frequently)

2) Grouped Data

The formula for the Mode is:

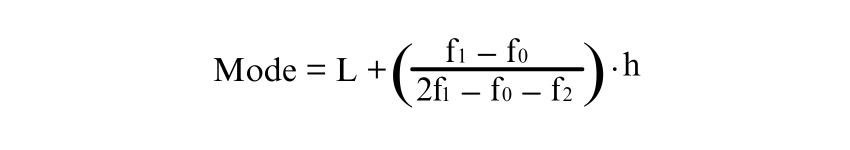
Where:

Steps to Calculate the Mean of a Data Set

The Mean is simply the average of all numbers in a data set

1) Add Up All the Values

Adding up all the values for the Mean:

a) This means summing up each number in your data set

Example: For the data 2,4,6,8:

2+4+6+8 = 20

2) Divide the Total by the Number of Values

Dividing the total by the number of values for Mean:

a) Take the total sum from Step 1 and divide it by the number of values in the set

Example: There are 4 values in the data set

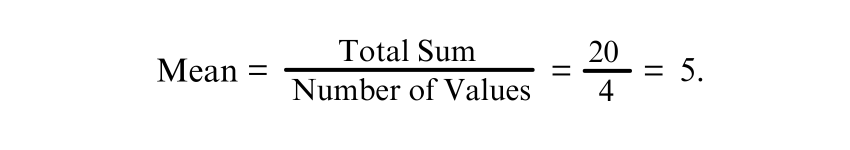
Answer: The Mean (average) of 2,4,6,8 is 5

Steps to Identify the Median

The Median is the middle value in a sorted data set. If the set has an even number of values, it’s the average of the two middle numbers.

1) Arrange Your Data in Order

Arranging the data in the order for the Median:

a) Sort all numbers in ascending order (from smallest to largest)

Example: Data set 7,3,5 → Sorted: 3,5,7

2) Find the Middle Value

Finding the middle values for the Median

If the number of values is odd:

a) The middle number is the Median

Example: For 3,5,7 → Median = 555

If the number of values is even:

a) Average the two middle numbers

Example: Data set 4,6,8,10:

Middle values = 6 and 8

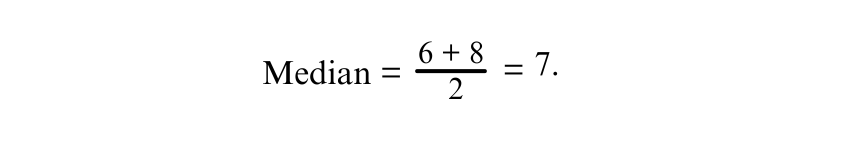
Answer: The Median is 7 for 4,6,8,10

3) Calculate the Mean of two Middle Values (if Necessary)

If a data set contains only four values, there isn't a single middle value when arranged in ascending order. For instance, consider the data set: 10, 12, 14, and 16. To find the Median, add the two middle values (12 and 14), resulting in 26. Then, divide this sum by 2 to get the Median value, which is 13.

Transform numbers into knowledge with our Mathematical Optimisation For Business Problems Course - Register today!

Steps to Find the Modal Value of a Data Set

The Mode is the number that occurs most frequently in the data set

1) Arrange the Data Set in Order

Arranging the data set in the order for Mode:

a) Organise the values from smallest to largest

Example: 5,3,3,4,6,3 → Sorted: 3,3,3,4,5,6

2) Identify the Value That Appears Most Frequently

Identifying the value that appears most frequently for Mode:

a) Look for the number that repeats the most

Example: In 3,3,3,4,5,6 the number 3 appears most often

Key Differences Between Mean, Median, and Mode

The following are the key differences between Mean, Median, and Mode:

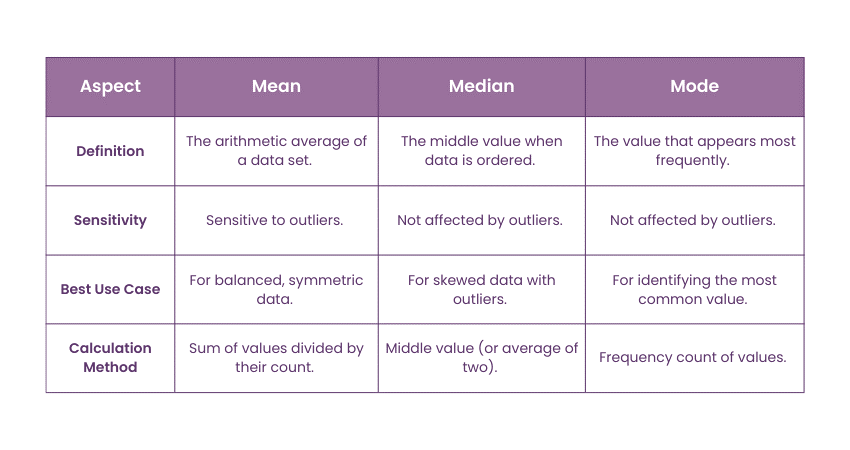
1) Definition:

a) Mean is the arithmetic average of a set of values, calculated by summing all the values and dividing by their count.

b) Median is the middle value in an ordered dataset or the average of the two central values if the dataset has an even number of entries.

c) Mode represents the value or values that occur most often within a dataset

2) Calculation:

a) Mean requires summing all data points and dividing by their total count

b) Median involves arranging the data in ascending order and identifying the central value(s).

c) Mode is determined by identifying the most frequently occurring value(s), requiring no arithmetic calculations.

3) Sensitivity to Outliers:

a) Mean is highly sensitive to outliers, which can skew its value significantly

b) Median is not affected by outliers and provides a better representation of central tendency for skewed data.

c) Mode is unaffected by outliers as it is based solely on frequency

4) Suitability for Data Types:

a) Mean is suitable for continuous or quantitative data

b) Median is ideal for ordinal, continuous, or skewed data distributions

c) Mode can be applied to both numerical and categorical data

5) Uniqueness:

a) Mean is always a single, unique value for a dataset

b) Median is a single value, except when the dataset is even, in which case it is the average of the two middle values.

c) Mode may not exist if no value repeats, and it can have multiple values if several values share the highest frequency.

Looking to ace your next interview? Check out these top Mean Stack Interview Questions and prepare like a pro!

Solved Examples on Mean, Median and Mode

Understanding Mean, Median, and Mode is crucial in statistics, as they help summarise data effectively. These measures of central tendency give insights into the distribution of values in a dataset. Below, we explore solved examples to clarify these concepts:

Example 1:

If the Mean of the following data is 25.4, find the missing frequency (p).

x	12	18	24	30	36
f	5	8	p	10	7

Example 2:

The Mean of 6 numbers is 22. If one number is excluded, their Mean becomes 20. Find the excluded number.

Example 3:

A survey on the heights (in cm) of 60 girls in a class was conducted, and the following data was obtained:

Height (in cm)	110-120	120-130	130-140	140-150	150-160	Total
Number of girls	3	9	15	18	15	60

Summary of When to Use the Mean, Median and Mode

When working with data, choosing the best measure of central tendency - Mean, Median, or Mode - depends on the type of variable and how the data is distributed. Here’s a quick guide to help you decide:

Conclusion

Grasping Mean Median Mode transforms raw data into meaningful stories. These statistical tools are your secret weapons for decoding everything from academic results to business metrics. By mastering them, you gain the ability to see beyond the numbers and make smarter, data-driven decisions.

Your journey into data begins here with our Statistics Course - Sign up today!