What is Standard Deviation in Statistics with Examples

Standard Deviation is a fundamental concept in Statistics that measures the amount of variation or dispersion in a set of data. It plays a crucial role in understanding data distribution and making informed decisions in various fields, from finance to science. The Standard Deviation measures the dispersion of data and quantifies data variability. Learn what is Standard Deviation and how to calculate it in this blog.

This blog will also examine Standard Deviation, exploring its definition, calculation methods, and practical applications. Read more to learn more!

Table of Contents 

1) What is  Standard Deviation? 

2) The purpose of Standard Deviation  

3) Steps for calculating the Standard Deviation by hand

4) Use cases of Standard Deviation  

5) Strengths of Standard Deviation 

6) Limitations and alternatives 

7) Conclusion 

What is Standard Deviation?  

Standard Deviation is a fundamental statistical measure that provides insight into the variability, dispersion, and distribution of Data Points within a dataset. It measures the spread out or clustered data values around the Mean or Average. In essence, Standard Deviation quantifies the degree to which individual Data Points deviate from the central tendency represented by the Mean. 

Mathematically, Standard Deviation is calculated by taking the square root of the Variance. Variance measures the average squared difference between each Data Point and the Mean. On the other hand, Standard Deviation brings this measure back to the original units of the data, making it more interpretable. 

A low Standard Deviation is an indication of the Data Points being close to the Mean, thus having little variability or dispersion. Conversely, a high Standard Deviation signifies that Data Points are more widely dispersed from the Mean, indicating greater variability in the dataset. 

Standard Deviation is widely used in various fields, including Statistics, finance, science, and social sciences. It helps in risk assessment, quality control, hypothesis testing, and data analysis, allowing researchers, analysts, and decision-makers to better understand and interpret data distributions.
 

The purpose of Standard Deviation  

The purpose of Standard Deviation can be summarised as follows: 

a) Quantifying variation: Standard Deviation precisely quantifies the dispersion of data points around the Mean. A high Standard Deviation indicates that data points are spread out over a wider range, while a low Standard Deviation suggests that data points are clustered closely around the mean. 

b) Identifying outliers: Standard Deviation assists in identifying outliers or extreme values in a dataset. Outliers can significantly affect data analysis and decision-making, and Standard Deviation helps flag them. 

c) Comparing datasets: Standard Deviation enables the comparison of variability between different datasets. It allows you to assess which dataset exhibits more or less variability, making it a valuable tool in various domains, including finance, quality control, and scientific research. 

Prepare for your next interview! Explore essential stakeholder management interview questions and answers now!

Steps for calculating the Standard Deviation by hand

Standard deviation is automatically computed by the statistical analysis software you employ. However, it can also be manually computed to gain a deeper comprehension of the underlying formula.

To manually determine the Standard Deviation, you can follow six primary steps. The following are the steps to be followed:

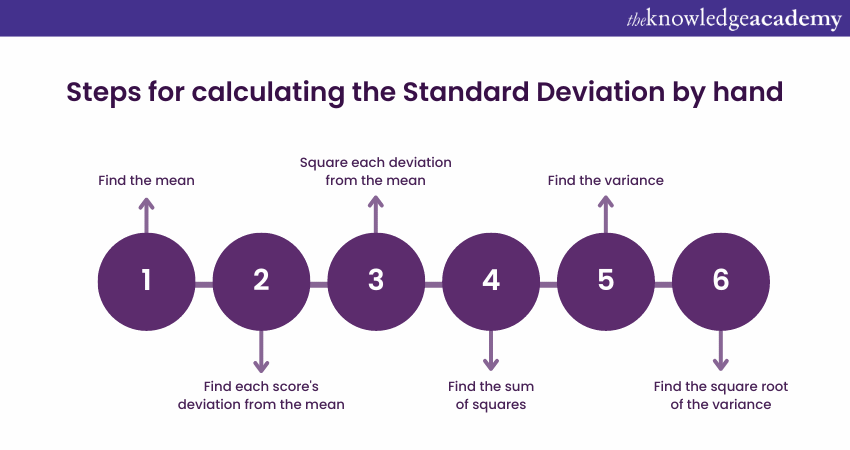
Step 1: Find the mean

To calculate the mean, you should sum up all the individual scores in your dataset and subsequently divide this sum by the total number of scores in the dataset. This process provides you with a central value that represents the average or typical value of the data.

For example, we have a dataset of exam scores for a class of five students: 85, 92, 78, 88, and 95. To find the mean, you would add these scores together: 85 + 92 + 78 + 88 + 95 = 438. Then, divide this total by the number of scores, which is 5. Therefore, the mean (average) score for this class is 438 ÷ 5 = 87.6. This means that, on average, the students in the class scored approximately 87.6 points on their exams.

Step 2: Find each score's deviation from the mean

To obtain the deviations from the mean, you should subtract the calculated mean value from each score in your dataset. This process helps you understand how each data point differs from the average or mean, indicating whether a data point is above or below the central tendency.

For example, in the case of the class's exam scores, we found that the mean score was 87.6. Now, to calculate the deviations from the mean for each student's score, you would subtract this mean value from each student's score. For instance, for the first student with a score of 85, the deviation from the mean is 85 - 87.6 = -2.6. For the second student with a score of 92, the deviation is 92 - 87.6 = 4.4. You repeat this process for each score in the dataset, which provides insights into how each student's performance compares to the class's overall average.

Build an effective stakeholder management plan! Learn the key steps to keep your project on track.

Step 3: Square each deviation from the mean

For each deviation from the mean, you should square the value. Squaring these deviations turns them into positive numbers and is an essential step in the calculation of the variance, a measure of the spread or variability within the dataset.

After determining the deviations from the mean for each student's score, we square each of these deviations. For example, for the first student with a deviation of -2.6, squaring it results in 6.76 (since -2.6 * -2.6 = 6.76), and for the second student with a deviation of 4.4, squaring it results in 19.36 (since 4.4 * 4.4 = 19.36). By squaring these values, you ensure that they are all positive and give more weight to larger deviations in your analysis.

Step 4: Find the sum of squares

Summing up all the squared deviations, referred to as the "sum of squares," is the next step in calculating the variance. The sum of squares quantifies the total variability within the dataset, considering the squared differences between each data point and the mean.

In our class's exam scores dataset, after squaring the deviations for each student's score, you would add these squared values together. For example, for the first student with a squared deviation of 6.76 and the second student with a squared deviation of 19.36, you would add these two values along with the squared deviations of all other students. This cumulative sum represents the "sum of squares," which measures the overall variation within the dataset.

Discover how stakeholder analysis can improve project success! Dive into our comprehensive guide.

Step 5: Find the variance

Divide the sum of the squares by n – 1 (for a sample ) or N (for a population) – this is the variance.

Step 6: Find the square root of the variance

This must be followed with finding the Standard Deviation. For this you can take the square root of the variance.

Use cases of Standard Deviation
 

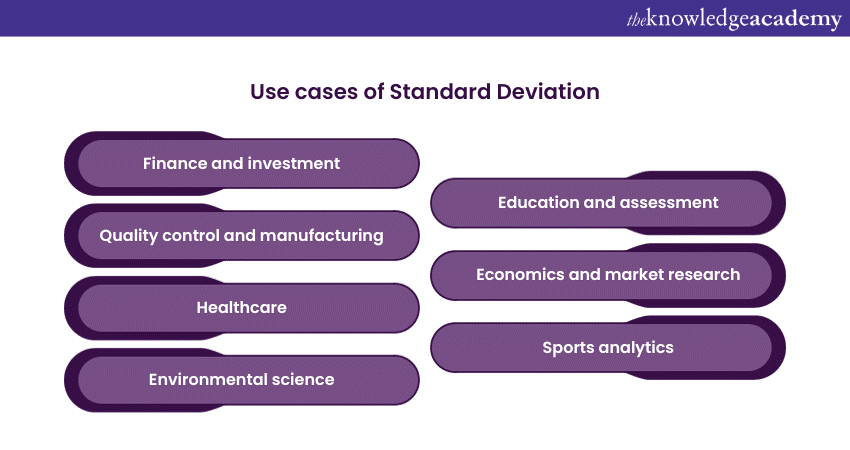
Standard Deviation is a versatile statistical measure with numerous real-life applications across various fields. It helps understand data variability, assess risk, and make informed decisions. Here are some of the use cases mentioned below: 

Finance and investment 

a) Portfolio risk assessment: Investors and financial analysts use Standard Deviation to measure the volatility of investment portfolios. A higher Standard Deviation indicates greater risk, helping investors make informed choices about diversification. 

b) Stock price volatility: Traders and analysts assess the volatility of stock prices using Standard Deviation. It aids in predicting market movements and making trading decisions. 

Quality control and manufacturing 

a) Product quality: Manufacturers use Standard Deviation to ensure consistent product quality. They can identify and address quality issues by measuring the variability of product dimensions or characteristics. 

b) Process control: In industries like semiconductor manufacturing, Standard Deviation helps monitor production processes to maintain tight control over specifications and minimise defects. 

Healthcare 

a) Medical research: Standard Deviation measures the variability in medical data, such as patient responses to treatment or the distribution of medical test results. Researchers use it to draw meaningful conclusions from clinical trials. 

b) Healthcare performance metrics: Hospitals and healthcare providers use Standard Deviation to assess patient outcomes and healthcare quality variations. It aids in identifying areas for improvement. 

Environmental science 

a) Climate data analysis: Environmental scientists use Standard Deviation to analyse climate data. It helps identify trends, extremes, and anomalies in temperature, rainfall, and other variables. 

b) Pollution monitoring: Standard Deviation is used to assess the variability of pollutant levels in air and water quality monitoring. It aids in identifying sources of pollution. 

Clarify stakeholder roles and responsibilities with our easy-to-follow guide. Get started now!

Education and assessment 

a) Test score analysis: Educational institutions and policymakers use Standard Deviation to evaluate student performance on standardised tests. It helps identify achievement gaps and assess the effectiveness of educational programs. 

b) Grading consistency: Teachers and grading committees use Standard Deviation to ensure consistent grading practices. It helps maintain fairness in assessment. 

Economics and market research 

a) Economic indicators: Economists use Standard Deviation to analyse economic data, such as inflation rates and GDP growth. It provides insights into economic stability and volatility. 

b) Consumer behaviour: Market researchers use Standard Deviation to analyse consumer preferences and behaviours. It helps businesses tailor their products and marketing strategies. 

Sports analytics 

a) Player performance: Sports analysts use Standard Deviation to evaluate player performance Statistics like scoring averages, assists, or rebounds. It helps teams make data-driven decisions like player recruitment or strategy adjustments. 

b) Team performance: Standard Deviation is used to assess the variability of team performance in various sports. It aids in ranking teams and predicting tournament outcomes. 

Unlock your potential in the world of business analysis with our Business Analyst Fundamentals Course. Register today! 

Strengths of Standard Deviation
 

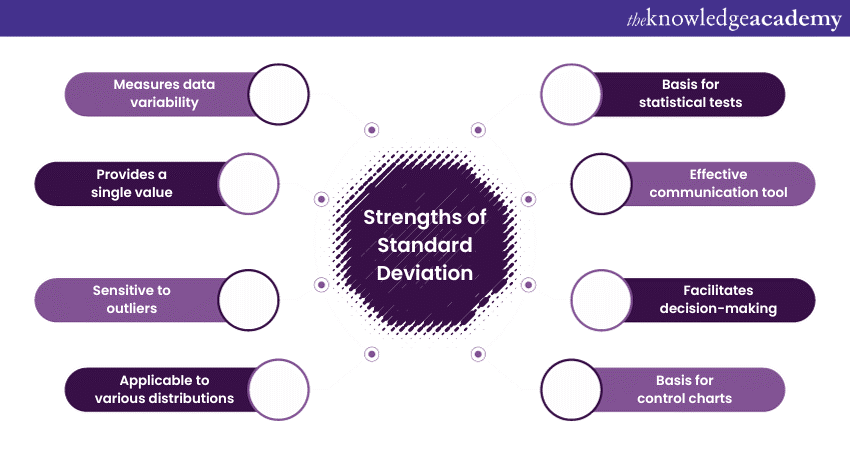
Standard Deviation, often denoted as σ (sigma) for population data and s for sample data, is a powerful statistical tool with several strengths that make it invaluable in data analysis and decision-making. Let's explore some of its key strengths: 

a) Measures data variability: Standard Deviation quantifies the spread or dispersion of Data Points within a dataset. It clearly indicates how individual Data Points deviate from the mean. A high Standard Deviation suggests that Data Points are widely scattered, while a low Standard Deviation indicates that Data Points are closely clustered around the mean. 

b) Provides a single value: Standard Deviation condenses the information about data variability into a single numerical value. This simplifies data interpretation and allows for easy comparison between datasets. For example, it helps compare the risk associated with different investment portfolios in finance. 

c) Sensitive to outliers: Standard Deviation is sensitive to outliers, which are extreme values that can significantly impact data distribution. This sensitivity helps in identifying and addressing anomalies in the dataset. It's particularly valuable in quality control processes to detect defective products in manufacturing. 

d) Applicable to various distributions: Standard Deviation is not limited to specific data distributions. It can be used with multiple types of data, including normal (bell-shaped), skewed, and multimodal distributions. This versatility makes it a widely applicable tool in numerous fields, including biology, economics, and social sciences. 

e) Basis for statistical tests: Standard Deviation serves as the foundation for many statistical tests, such as hypothesis testing and ANalysis Of VAriance (ANOVA). These tests rely on the square of the Standard Deviation or variance. 

f) Effective communication tool: Standard Deviation facilitates effective communication of data characteristics. When presenting findings or making decisions, expressing data variability through Standard Deviation helps stakeholders grasp the uncertainty or risk associated with the data. 

g) Facilitates decision-making: In fields like finance, where risk assessment is paramount, Standard Deviation is instrumental in making informed decisions. For instance, investors use it to assess the volatility of financial assets and evaluate potential investments. 

h) Basis for control charts: In quality control and process monitoring, control charts are essential tools. Standard Deviation forms the basis for control limits on these charts, helping organisations detect process variations and maintain consistent quality.

Curious about business analyst salaries? Find out the latest data and trends in your region now!

Limitations and alternatives to Standard Deviation 

While Standard Deviation is a powerful tool for measuring the spread or dispersion of data, it's essential to understand its limitations and consider alternatives when they better suit the data or research objectives. 

Limitations of Standard Deviation 

a) Sensitivity to outliers: Standard Deviation has high sensitivity to outliers or extreme values in the data. A single outlier can significantly inflate the Standard Deviation, potentially misrepresenting the data's overall variability. 

b) Assumption of normal distribution: Standard Deviation assumes the data follows a normal distribution. In cases where the data distribution is significantly skewed or abnormal, Standard Deviation may not accurately capture variability. 

c) Units of measurement: Standard Deviation is expressed in the same units as the data, making it challenging to compare the variability of data with different units of measurement. 

d) Sample size dependency: The formula for sample Standard Deviation (using "n-1" in the denominator) depends on sample size. Smaller samples yield more significant Standard Deviations, which can be misleading when comparing datasets of varying sizes. 

Alternatives to Standard Deviation 

a) Variance: Variance is the square of the Standard Deviation and measures data dispersion. It shares many limitations as Standard Deviation, but is sometimes preferred when dealing with positive data, as it ensures all values are positive. 

b) Range: The range is the most straightforward measure of dispersion. It is calculated as the difference between the maximum and minimum values in the dataset. While it's easy to calculate, it's sensitive to outliers and may not provide a complete picture of variability. 

c) Interquartile Range (IQR): IQR is a robust measure of spread focusing on the middle 50% of data, excluding outliers. It's calculated as the difference between the 75th percentile and the 25th percentile of the data. IQR is less affected by extreme values than Standard Deviation. 

d) Coefficient of Variation (CV): CV measures relative variability by expressing the Standard Deviation as a percentage of the Mean. It's useful when comparing datasets with different means or units of measurement, as it standardises variability. 

e) Mean Absolute Deviation (MAD): MAD calculates the average absolute difference between each Data Point and the Mean. It provides a measure of variability less sensitive to extreme values than Standard Deviation. 

f) Median Absolute Deviation (MAD-Median): MAD-Median is like MAD but uses the median instead of the mean. It's particularly robust against outliers and skewed distributions.  

Conclusion 

Standard Deviation is more than just a statistical term—it's a key to unlocking insights from data. You've taken a significant step towards becoming a data-savvy individual by comprehensively exploring its definition, calculation methods, and applications. Irrespective of your use case and domain, Standard Deviation is your trusted companion in Statistics and data analysis.

Learn the roles and responsibilities of a Business Analyst with our Certified Business Analyst Professional (CBA – PRO)