Binary Tree Data Structure: Explained

In computer science, there are different ways to organise data. Binary Tree Data Structure is one such way to structurally organise data in a system. The main use of these Binary Trees in computer programs is to build software, organise large amounts of data and build smart computing systems. In this blog, you will understand everything about Binary Tree Data Structure, its key components, types, benefits and more.   

Table of Contents 

1) What is Binary Tree Data Structure? 

2) Terminologies used in Binary Tree 

3)  Implementation of a Binary Tree Data Structure 

4) Types of Binary Trees 

5)  Applications of Binary Tree Data Structure 

6)  Benefits of using Binary Tree 

7) Drawbacks of Binary Tree 

8) Conclusion 

What is Binary Tree Data Structure?
 

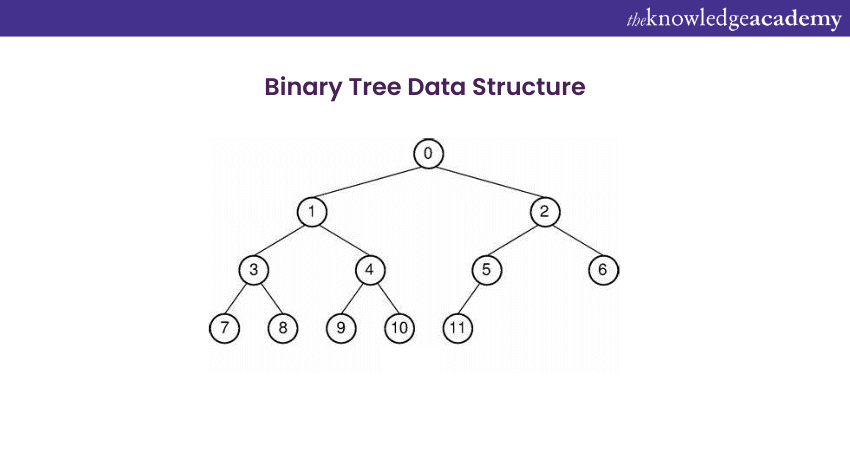
Binary Tree Data Structure is a non-linear type of data structure which is very commonly used in computer science. Binary Trees include a starting point known as the root. The root node can have the highest of two nodes; every node that holds two sub-nodes is called a parent node. The sub-nodes are commonly called child nodes, including one left child and one right node.      

Want to learn more about Data Structure? Sign up for our Data Structure and Algorithm Training

Terminologies used in Binary Tree 

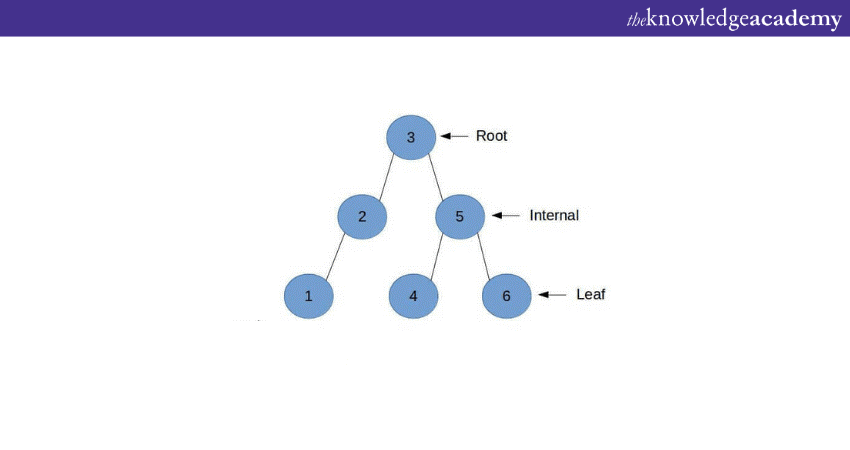
Let’s understand some of the key terminologies used in a Binary Tree. These terminologies represent crucial components of the Binary Tree Data Structure.   

a) Root: A root is the topmost node in the tree. All other nodes descend from the root node.  

b) Parent Node: Any node can have a maximum of two sub-nodes or child nodes. A node can have zero child nodes as well. However, only if a node has a child node can be called as a parent node.  

c) Internal Node: Internal nodes are those nodes that have at least one child node.     

d) Subtree: In big tree structures, a Subtree is a part of the larger tree. It starts from a node and consists of all the descendant nodes.   

e) Height of Node: The height of a tree is the maximum depth of a node in the tree structure. In other words, it can also refer to the maximum number of nodes a tree can reach.  

f) Binary Search Tree (BST): This is a special type of tree that is used to search, insert, and delete elements. In Binary Search Tree, the right child node contains more value than the node. Meanwhile, the left child node contains a value less than the node.   

g) Traversal: It is a technical process to visit each node in the tree structure. This process has different types based on the order, such as in-order, pre-order, and post-order. 

Implementation of a Binary Tree Data Structure 

The implementation of Binary Tree can be classified into two classes: ‘Node’ and ‘BinaryTree’. Let's understand the implementation of these classes with the following steps:   

Node class  

The ‘Node’ class represents a single node in the Binary Tree. Each of the nodes contains a value, which is represented by ‘va1’ and pointers to its left and right children, which are represented as ‘left’ and ‘right’.    

BinaryTree class 

The ‘BinaryTree’ class is the main structure that manages the Binary Tree. It includes a ‘root’ attribute, which refers to the topmost node in the structure. Initially, the ‘root’ is set to ‘None’, indicating an empty tree.    

Insertion operation 

The ‘insert’ method is used to add notes to the Binary Tree. If the tree is empty, a new node with a value becomes the root. If the tree is not empty, the ‘insert’ method is used to find the correct position of the new node based on its value.   

Private insert method 

The ‘insert’ method is a private recursive function used by the ‘insert’ method. It compares the value of the current node with the value of the node to determine whether to go left or right in the tree until an appropriate portion is found.   

Inorder traversal 

The ‘inorder_traversal’ method is used to traverse the tree in an inorder manner. In order traversal, the first visit is the left subtree, then the current node and finally the right subtree.   

  

 

Types of Binary Trees 

Binary Tree is available in various types based on the characteristics and application of the Data Structure. To understand some of the common types of Binary Tree, we need to look into each in detail:

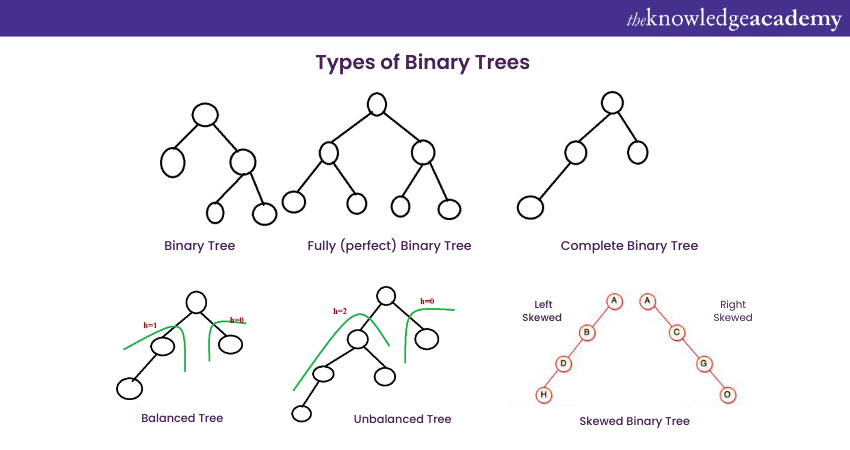
Full Binary Tree 

In a Full Binary Tree, each node has either zero or two child nodes. Nodes in this type of Binary Tree cannot have any one node, and if it has nodes, it must have both nodes or none. One of the main advantages of this type of tree is that it allows efficient searching and organising operations. The depth of a Full Binary Tree is kept to a minimum, which helps in faster data retrieval. 

Complete Binary Tree 

A Complete Binary Tree has all levels of the tree filled except the last one. This type of tree is characterised by the last level, where all the keys are positioned in the leftmost possible node, giving it a complete look. A complete Binary Structure is useful to implement priority queue and heap Data Structure.   

Perfect Binary Tree 

A type of Binary Tree with all the nodes having exactly two nodes and all the leaf nodes situated at the same level is described as a Perfect Binary Tree. This type of tree has a symmetrical and balanced structure. These trees perform very well in operations like searching, sorting and data retrieval. Apart from their efficiency and balanced structure, they can be resource intensive as they require a specific number of nodes, each with a power of two.      

Degenerate Binary Tree 

Degenerate Binary Tree is also known as Pathological Tree. This type of tree has all the internal nodes with only a child. A Degenerate Binary Tree creates a structure that essentially looks like a linked list where each node is in a linear fashion. This type of tree is not effective to be used for data retrieval and searching operations. However, they can be used where the data is present in a linear format. 

Balanced Binary Tree 

A Balanced Binary Tree is a type of Binary Tree in which the height of the left and right sub-node does not differ from each other by more than one node. This type of Data Structure ensures that the tree remains flat and enables efficient searching, inserting and deleting nodes. Balanced Binary Trees are primarily used for cases where predictable performance is important. 

Skewed Binary Tree 

Skewed Binary Trees are specific types of trees which are either entirely skewed to the left or the right side. In the left-skewed tree, all the nodes have a left child; meanwhile, in the right-skewed tree, all the nodes have a right child. This type of tree is sometimes considered a type of Degenerated Binary Tree as they both have a linear behaviour for operations.   

Applications of Binary Tree Data Structure 

Binary Tree demonstrates a wide range of applications based on its utility and importance in various field of computer science and engineering. Some of the most crucial applications of the Binary Tree are as follow: 

Binary Search Tree (BST) 

This is one of the most profound applications of Binary Trees is in the for of Binary Search Tree (BST). These trees are used in efficient searching, insertion, and deletion operation. BST are primarily used in dictionaries, databases and file system because of its data sorting capabilities.
 

Heap Data Structure
 

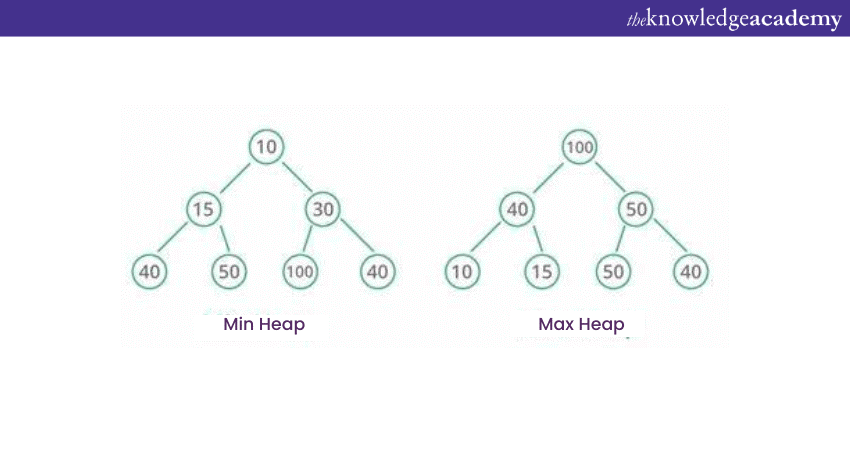
Binary Tree in the form of Binary Heap has a variety of applications. The priority queue is one of the main applications where elements with different priority are managed and organised. It is also used in optimising resource allocation with its capability of extracting highest or lowest priority element.  

Huffman coding Tree
 

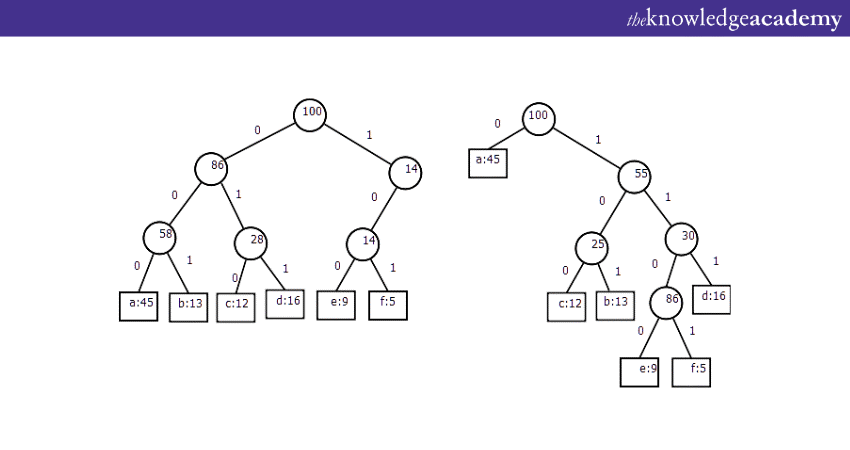
One of the fundamental applications of Binary Tree is compression of data algorithms particularly in Huffman coding. This technique is assigning variable length of codes to elements in the tree based on their frequency of occurrence. By using the application of Binary Tree in Huffman coding, organisations can efficiently store and transmit data.   

Parsing expression and evaluation 

Using the parsing expression and evaluation application Binary Tree efficiently represent the mathematical expression primarily in the field of compilers and interpreters. This enables compilers to efficiently parse and evaluate complex expression in programming language. With the use of expression tree, compilers can make accurate execution of mathematical expression in software development. 

Learn more about Programming Languages to make a significant effect in the software world with our Programming Training 

Decision Tree in Machine Learning 

Decision Tree is a specialised application of Binary Tree which are widely used in data mining and Machine Learning. These trees facilitate the process of classification and regression by allowing the algorithm to make decision based on the attributes of data. Decision Tree contributes to the advancement of systems in various domains like healthcare and data analysis. 

Benefits of using Binary Tree 

The use of Binary Tree provides a powerful tool for efficiently managing, organising and accessing the data in a wide range of operations across computer science and engineering. Some of the key benefits of Binary Tree Data Structure are:  

Optimising data storage 

Binary Tree is very efficient in managing and organising data in a sorted order. This use case is valuable when the data needs to be arranged based on specific requirements. For example, in an address book application a Binary Search Tree (BST) can store the contacts alphabetically allowing for easy and quick access to specific entries.  

Priority queue implementation 

Binary heaps are specialised form of Binary Tree which are widely used for implementing priority queue. This is useful in applications like operating systems. Algorithms and event-driven systems.  

Efficient traversal 

Binary Tree supports various transversal methods, which are useful in operations like printing the element in a sorted order. It also performs mathematical operations on expressions represented as trees and navigates directory structures in any file system.    

Efficient insertion and deletion 

The Binary Search Tree is efficient in addition and deletion of data operation. If balanced properly, these operations can be performed in logarithmic time. This property makes BSTs suitable for dynamic data sets where elements are frequently added or removed, such as file system and priority queue. 

Hierarchical representation 

Binary Tree naturally represents data in a hierarchical structure. This makes Binary Tree Data Structure useful for modelling relationships between nodes in organisational charts, family trees and file directory structures. 

Data distribution 

In use cases where the data distribution is unpredictable, balanced tree help ensure that operation remain efficient, independent of the amount of input data. This is particularly useful for applications like databases where maintaining consistency in performance is crucial. 

Drawbacks of Binary Tree Data Structure  

While Binary Tree Data Structure offers a variety of benefits, it does have some limitations as well. It is important to discuss these limitations to understand the capabilities of Binary Trees: 

Inefficient for dynamic data 

Binary Tree might not be the best choice for dynamic data sets. If the size of the data is not known in advance the process of managing the data can be not so efficient. In cases where the frequent additions and removals of elements occur, the overhead of balancing operations can offset the advantage of using a Binary Tree. 

Memory overhead 

Binary Tree is not efficient and might incur a high memory overhead as compared to other Data Structures. Each node in the Binary Tree requires an extra memory to store pointers and references to its left and right child nodes. This overhead can be significant, especially in the cases where memory efficiency is crucial.  

Unbalanced degeneration 

Binary Tree can be unbalanced or degenerated in terms of performance. In some cases, the Binary Tree can degenerate into a linked list which can cause the rendering search, insertion and deletion operations less efficient. This mainly happens when the nodes are inserted in a sequential order making the tree grow in linear order.  

Limited functionality 

Binary Tree Data Structure are designed for one dimensional data. While dealing with multi-dimensional data like geographical data, Binary Tree might not be the most preferable choice. This limitation of makes Binary Tree a less reliable structure while dealing with multi-dimensional data. Specialised Data Structures like Quad Trees or k-d Trees can be a more efficient choice while dealing with this type of data.  

Lack of native support 

Binary Tree do not have a native support for operations like finding the minimum or maximum elements in a given time. While these operations can be implemented with Binary Tree, they might require additional bookkeeping or transversal which can be a complex and time-consuming process.   

Conclusion 

A Binary Tree Data Structure is a hierarchical structure that is efficiently used in organising and managing large sets of data. These structures serve as a fundamental concept in computer science and programming. We hope that this blog helped you understand the key components, applications and other valuable intricacies of Binary Tree. 

Unlock the potential of Data Structure with Python – Register for our Python Programming Training and get started today!