We may not have the course you’re looking for. If you enquire or give us a call on +65 6929 8747 and speak to our training experts, we may still be able to help with your training requirements.
Training Outcomes Within Your Budget!
We ensure quality, budget-alignment, and timely delivery by our expert instructors.

The Isosceles Triangle, with its two equal sides and distinct base, is a geometric marvel that frequently appears in both architectural masterpieces and academic problems. Calculating its area might seem daunting at first, but with the right approach, it becomes an intriguing and manageable task.
In this blog, we’ll explore the geometrics behind Isosceles Triangles, uncover their unique properties, and provide clear, step-by-step methods for calculating their area. We’ll also highlight real-life examples to solidify your understanding and appreciation of this elegant shape.
Table of Contents
1) What is the Area of an Isosceles Triangle?
2) Formulas for the Area of an Isosceles Triangle
3) Area of Isosceles Triangle Using Sides
4) Area of Isosceles Triangle Using Heron's Formula
5) Area of Isosceles Triangle Using Trigonometry
6) Area of an Isosceles Right Triangle
7) Area of Isosceles Triangle Examples
8) Conclusion
What is the Area of an Isosceles Triangle?
The area of an Isosceles Triangle indicates the space enclosed by its sides in a two-dimensional plane. An Isosceles Triangle is characterised by having two equal-length sides, which correspond to two equal angles. Here are some distinctive properties of Isosceles Triangles:
a) The two equal sides are the legs; the angle formed between them is called the vertex or apex angle.
b) The side opposite the vertex angle is referred to as the base, and the angles adjacent to the base are known as base angles, which are also equal.
c) A perpendicular line drawn from the vertex angle to the base bisects both the base and the vertex angle, creating two congruent segments and angles.
Formulas for the Area of an Isosceles Triangle
Several formulas can be utilised to compute the area of an Isosceles Triangle depending on the information available. The most common formula is:
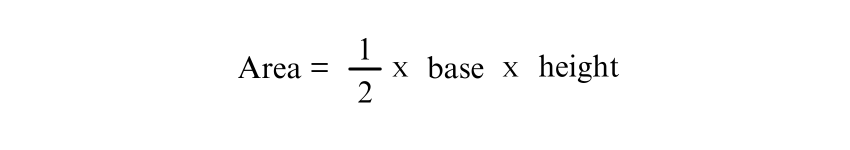
Other formulas may involve using the lengths of the sides or the angles, which we will discuss in detail.
Area of Isosceles Triangle Using Sides
If the lengths of the equal sides and the base of an Isosceles Triangle are known, you can calculate the height or altitude of the triangle. The formula for determining the area of an Isosceles Triangle using just the lengths of its sides is:
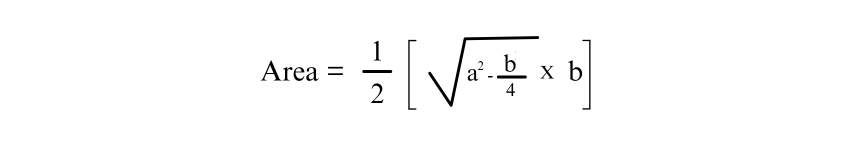
Where:
b = base of the Isosceles Triangle
h = height of the Isosceles Triangle
a = length of the two equal sides
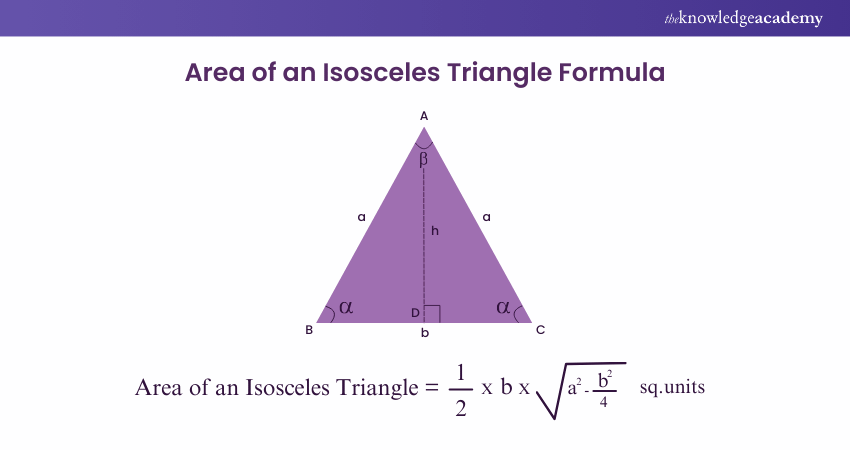
Area of Isosceles Triangle Using Heron's Formula
Heron's formula offers a way to calculate the area of any triangle when all three sides are known, including Isosceles Triangles. The formula is expressed as:
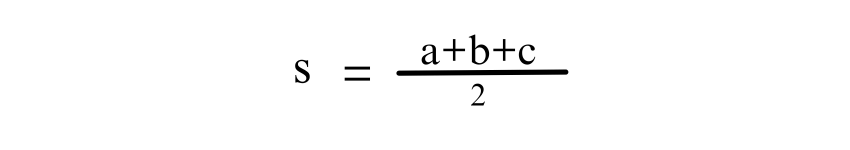
Where s is the semi-perimeter, the area can then be calculated using:
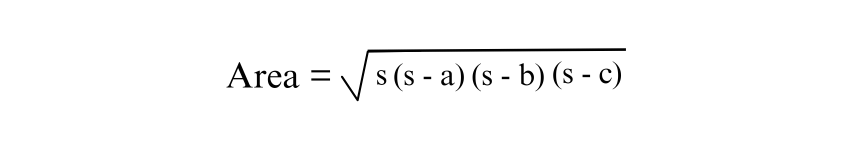
This method is invaluable for situations where the height is not readily available, providing a straightforward means of calculation.
Area of Isosceles Triangle Using Trigonometry
Trigonometry offers another way to calculate the area of an Isosceles Triangle, particularly when the angle between the two equal sides is known. The formula is:
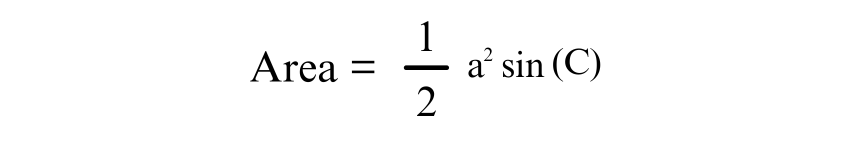
Where a is the length of the equal sides, and C is the angle between them. This approach is particularly useful in advanced geometry and physics applications.
Area of an Isosceles Right Triangle
An isosceles right triangle, with both legs of equal length, simplifies the area calculation:
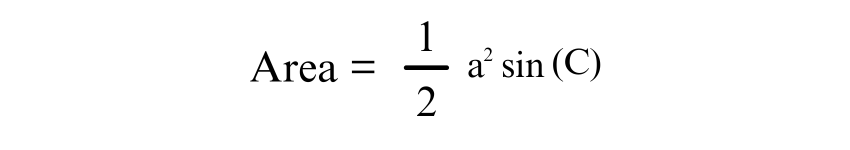
This specific case of the Isosceles Triangle highlights the unique properties of right angles and equal sides, making calculations straightforward and intuitive.
Enhance your communication skills with our Active Listening Training. Join now!
Area of Isosceles Triangle Examples
This section will explore practical examples of calculating the Area of Isosceles Triangles, showcasing various scenarios and methods. These examples will help firm your understanding of the concepts and formulas discussed earlier, making it easier to apply them in real-world situations.
1) Given Base Length and Height
Let’s consider an Isosceles Triangle with a base of 10 cm and a height of 8 cm. The area can be calculated as follows:
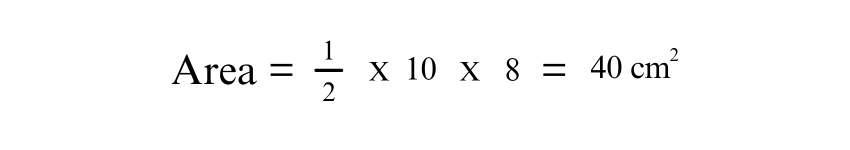
2) Given Base Length and Height (Alternate)
For an Isosceles Triangle with a base of 12 cm and height of 5 cm:
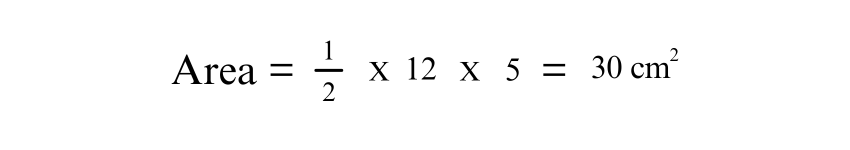
3) Compound Shapes
Imagine a compound shape where the base of the Isosceles Triangle is 8 cm, the triangle's height is 6 cm, the rectangle's length is 8 cm, and its width is 4 cm.
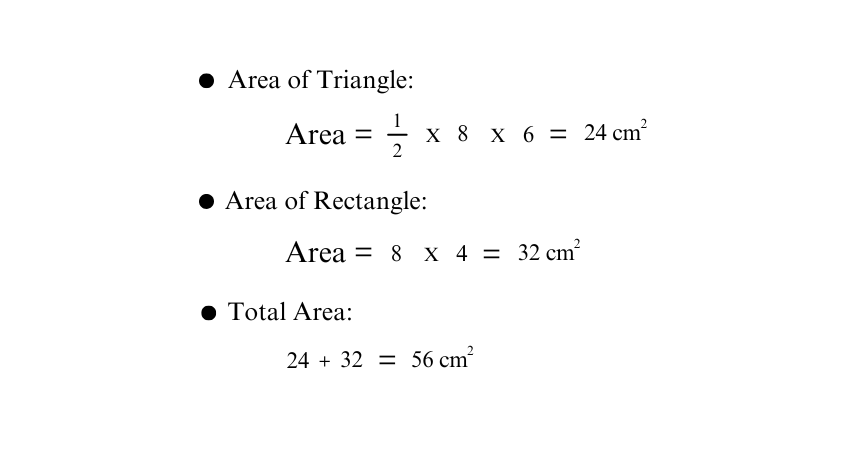
By adding both areas, you get the total area of the compound shape.
4) Finding Missing Height
Given the base of 14 cm and area of 48 cm², the height can be found using the area formula:
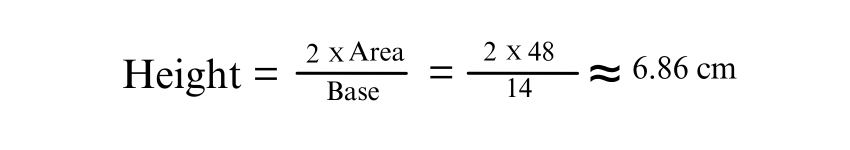
5) Word Problems
Word problems involving the area of an Isosceles Triangle require applying geometric concepts to real-life situations. Here's an example:
Problem:
A gardener wishes to create a triangular flower bed shaped like an Isosceles Triangle. The triangle's base is 16 m, and the area is 48 m². What is the height of the flower bed?
Solution:
To find the height, use the standard area formula for a triangle:

Answer:
The flower bed is 6 metres high. This approach showcases how understanding the area formula can help solve practical problems, such as designing a garden layout efficiently.
Enhance your efficiency with our Time Management Training. Join now!
Conclusion
Understanding the Area of the Isosceles Triangle unlocks a world of geometric possibilities, enhancing our appreciation for shapes and their properties. Calculating the Area of Isosceles Triangles with various methods and formulas becomes straightforward. Whether you're a student or a geometry enthusiast, mastering the Area of the Isosceles Triangle can greatly enrich your mathematical toolkit.
Increase your productivity with our Speed Writing Course – Join now!
Frequently Asked Questions

You can use Heron's formula or the formula involving the lengths of the sides. These methods allow you to calculate the area without directly measuring the height.

An Isosceles Triangle contains two equal sides, while an isosceles right triangle has a right angle (90 degrees) between those equal sides, making its area calculation simpler.

The Knowledge Academy takes global learning to new heights, offering over 30,000 online courses across 490+ locations in 220 countries. This expansive reach ensures accessibility and convenience for learners worldwide.
Alongside our diverse Online Course Catalogue, encompassing 19 major categories, we go the extra mile by providing a plethora of free educational Online Resources like News updates, Blogs, videos, webinars, and interview questions. Tailoring learning experiences further, professionals can maximise value with customisable Course Bundles of TKA.

The Knowledge Academy’s Knowledge Pass, a prepaid voucher, adds another layer of flexibility, allowing course bookings over a 12-month period. Join us on a journey where education knows no bounds.

The Knowledge Academy offers various Personal Development Courses, including Engineering Skills Training, Time Management Training and Active Listening Training. These courses cater to different skill levels and provide comprehensive insights into the Area of a Circle.
Our Business Skills blogs cover a range of topics related to Personal Development, offering valuable resources, best practices, and industry insights. Whether you are a beginner or looking to advance your Engineering Skills, The Knowledge Academy's diverse courses and informative blogs have got you covered.
Upcoming Business Skills Resources Batches & Dates
Date
 Engineering Skills Training
Engineering Skills Training
Fri 24th Jan 2025
Fri 21st Mar 2025
Fri 2nd May 2025
Fri 27th Jun 2025
Fri 29th Aug 2025
Fri 3rd Oct 2025
Fri 5th Dec 2025







 Top Rated Course
Top Rated Course



 If you wish to make any changes to your course, please
If you wish to make any changes to your course, please


