Types of Trees in Data Structures: A Comprehensive Overview

Exploring Types of Trees in Data Structure unveils a fundamental landscape crucial for efficient information management. Trees, with their hierarchical arrangement of nodes, play a pivotal role in organising and optimising algorithms.   

Exploring the nuances of these types will equip you with the foundational knowledge necessary for navigating the intricate world of Data Structures and leveraging their diverse applications in computational problem-solving. This blog shall help you learn that a tree in Data Structures is a hierarchical Data Structure consisting of nodes connected by edges and different types of such trees. 

Table of Contents 

1) What is a tree in Data Structure? 

2)  Different Types of Trees in Data Structure 

     a)  Binary Tree 

     b) Binary Search Tree 

     c) Ternary Tree 

     d) AVL Tree 

     e) Red-Black Tree 

     f) Segment Tree 

    g) N-ary Tree 

    h) B-Tree 

3) Conclusion 

What is a tree in Data Structure? 

A tree is a hierarchical and widely utilised organisational model that consists of nodes connected by edges, forming a structure reminiscent of natural trees. The root node is at the tree's apex, serving as the starting point for traversing the structure. Each node in the tree may have zero or more child nodes, creating parent-child relationships that define the hierarchy. 

Additionally, one of the defining features of trees is their branching structure, where nodes with no children are termed leaves, while nodes with at least one child are internal nodes. The depth of a node represents its distance from the root, and the tree's height is the length of the longest path from the root to a leaf.   

Moreover, these characteristics contribute to the efficiency of various algorithms and operations performed on tree structures. Trees have extensive applications in diverse fields of computer science, providing elegant solutions to problems ranging from efficient data retrieval to hierarchical representation of information. In contrast, Linear Data Structures offer different advantages and are essential for understanding how tree structures fit into the broader landscape of data organization and algorithm design. 

Whether it's binary trees for simple organisation, balanced trees for optimised search operations, or tries for efficient string storage, the concept of a tree in Data Structures remains a fundamental and versatile tool, offering a rich foundation for the design and implementation of algorithms and databases. 

Different Types of Trees in Data Structure 

In Data Structures, trees are nothing but hierarchical models pivotal for organising and managing data. Binary trees, including AVL and Red-Black trees, offer simplicity and balance. Multiway trees like B-trees and B+ trees handle large datasets effectively.   

Tries, like radix trees, specialise in storing and retrieving dynamic sets of strings. Each type serves distinct applications, contributing to computational efficiency. Below are the various types explained in detail: 

1) Binary Tree  

A Binary Tree in Data Structure is a fundamental hierarchical data structure composed of nodes, where each node has at most two children, referred to as the left and right subtrees. The topmost node is the root, and nodes without children are leaves.   

More importantly, Binary Trees are efficient for search and retrieval operations, facilitating data organisation that enhances computational efficiency. Their simplicity and versatility make them a cornerstone in various algorithms and applications in Computer Science.
 

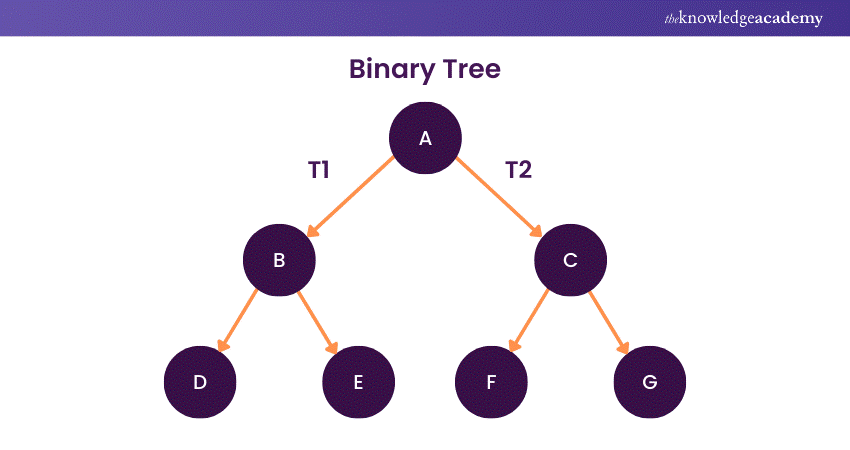
Now, Binary Trees comprise two main types depending on the number of children: 

a) Full Binary Tree: A Full Binary Tree is a binary tree in which every node has either 0 or 2 children, ensuring that each level is filled except possibly for the last, and all nodes are as left as possible. Such a structure in Computer Science optimises storage and retrieval. 

b) Degenerate Binary Tree: A Degenerate Binary Tree, also known as a pathological or skewed tree, is a binary tree in which each parent node has only one associated child, resulting in a structure akin to a linked list. Degenerate Binary Trees lack the balance property, impacting the efficiency of search and retrieval operations. 

Furthermore, Binary Trees can also be segregated into the following types based on their completion of levels: 

a) Complete Binary Tree: A Complete Binary Tree is a binary tree where all levels, except possibly the last, are fully filled, and all nodes are left as far as possible. This unique structure is maintained by filling levels from left to right, making storage, retrieval, and insertion operations efficient in computer science applications. 

b) Perfect Binary Tree: A Perfect Binary Tree is a specialised binary tree where all internal nodes have exactly two children, and all leaf nodes are at the same level. This balanced structure results in a complete and full binary tree, enhancing efficiency in data storage, retrieval, and traversal algorithms. 

c) Balanced Binary Tree: A Balanced Binary Tree is a binary tree in which the depth of the two subtrees of every node differs by at most one. This self-adjusting structure, such as AVL or Red-Black trees, ensures efficient search, insertion, and deletion operations, maintaining logarithmic time complexity in various applications. 

2) Binary Search Tree 
 

A Binary Search Tree (BST) is a specialised Binary Tree where each node has at most two children, and the left child is less than the parent, while the right child is greater. This ordering property enables efficient searching, insertion, and deletion operations, making BSTs valuable in Data Structures.  

Moreover, the logarithmic height ensures optimal performance, and the BST's simplicity and versatility make it a key choice for maintaining sorted collections and implementing various algorithms in Computer Science, offering a balance between simplicity and efficiency for storing and retrieving data. 

3) Ternary Tree  

A Ternary Tree is a hierarchical data structure where each node can have up to three children, distinguishing it from binary trees. This unique characteristic allows nodes to branch into three subtrees, providing additional flexibility in organising and representing hierarchical relationships.   

Moreover, Ternary Trees find applications in various scenarios, such as spell-checking algorithms, expression trees, and hierarchical representations. While less common than binary trees, the ternary structure accommodates richer relationships between nodes, expanding the scope of potential use cases.   

Understanding and implementing Ternary Trees offers a nuanced approach to hierarchical data representation, catering to scenarios where a triadic relationship is more fitting than the binary alternative. 

4)  AVL Tree
 

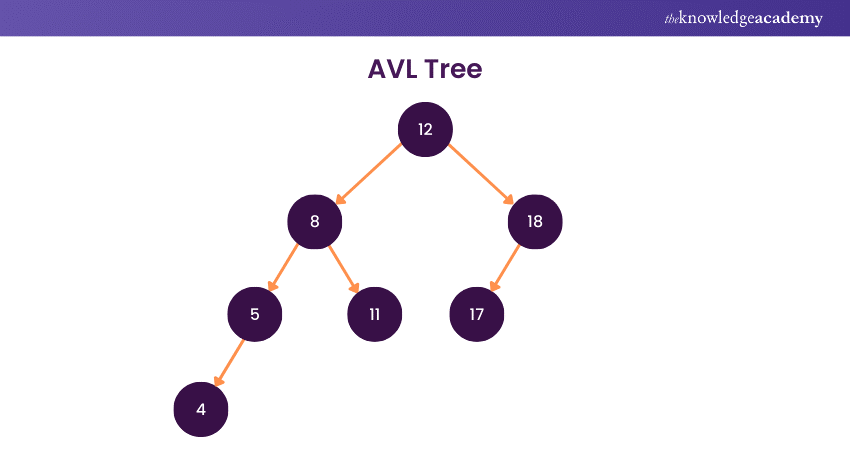
An AVL Tree is a self-balancing binary search tree, ensuring that the height difference between every node's left and right subtrees is at most one. Named after its inventors, Adelson-Velsky and Landis, an AVL Tree automatically adjusts its structure through rotations during insertion and deletion operations, maintaining logarithmic height and efficient search, insertion, and deletion times.   

More importantly, this balancing property enhances the performance of operations, making AVL Trees valuable in scenarios where optimal time complexity is critical, such as database indexing.   

While the maintenance of balance introduces additional overhead, the benefits of predictable performance make AVL Trees a powerful and widely used data structure in computer science for scenarios requiring fast and reliable search operations. Familiarity with Data Structures Interview Questions can be particularly useful, as it helps in understanding the nuances of AVL Trees and preparing for discussions on their implementation and advantages.  

Get equipped with the necessary programming knowledge by signing up for our Programming Training now! 

5) Red-Black Tree
 

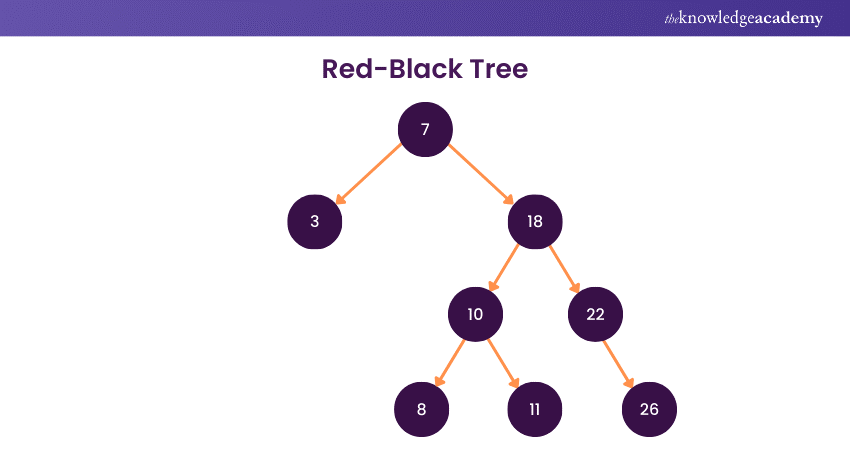
A Red-Black Tree is a self-balancing binary search tree with the key innovation of assigning colours (red or black) to its nodes. This colour-coding scheme ensures the tree remains approximately balanced, limiting the maximum path length from the root to any leaf.   

Additionally, the Red-Black Tree maintains five essential properties: 

a) The roots and leaves are black 

b) No two consecutive red nodes exist along a path 

c) Every path from a node to its descendant leaves has the same number of black nodes 

These properties ensure logarithmic height, guaranteeing efficient search, insertion, and deletion operations with a predictable time complexity.  

Red-black trees balance the simplicity of binary trees and the strict balancing of AVL Trees. The colour-coding mechanism reduces the frequency of rotations needed during insertion and deletion, leading to improved performance in practice.   

This makes Red-Black Trees particularly suitable for scenarios where a balance between structural integrity and operational efficiency is crucial, such as in implementing Data Structures like sets and maps in various programming languages. 

6) Segment Tree
 

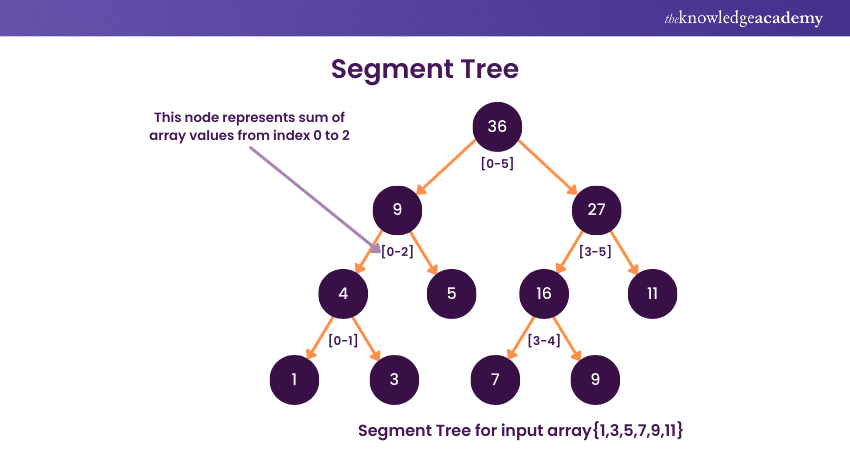
A Segment Tree is a versatile and efficient data structure for solving range query problems on an array or a list. It recursively divides the input array into segments or intervals, represented by nodes in the tree.   

Each node stores information summarising the data within its corresponding segment. Common applications of Segment Trees include range sum queries, range minimum/maximum queries, and other associative operations.  

Further, constructing a Segment Tree involves a bottom-up approach, where leaf nodes represent individual elements, and each parent node aggregates information from its children. This process ensures logarithmic query time complexity.   

Additionally, Segment Trees are dynamic, allowing for easy updates to individual elements in the underlying array without reconstructing the entire tree. The ability to efficiently handle a variety of range queries makes Segment Trees valuable in fields such as computational geometry, database systems, and competitive programming. A thorough understanding of Data Structures and Algorithms enhances your ability to effectively implement and apply Segment Trees in these scenarios.    

Despite their apparent simplicity, Segment Trees offer an elegant solution to complex problems involving large datasets and dynamic updates, showcasing their significance in algorithmic design and optimisation. 

7) N-ary Tree
 

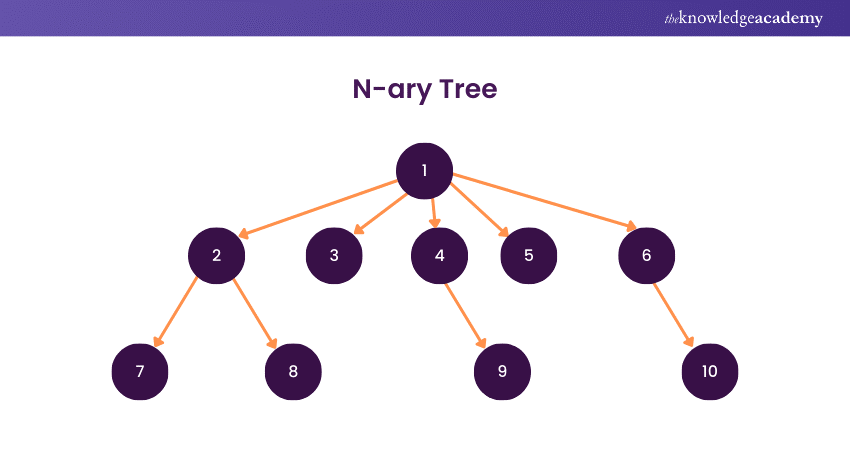
An N-ary Tree is a generalisation of binary trees where each node can have up to N children, providing a more flexible and scalable hierarchical structure. In contrast to binary trees, N-ary Trees accommodate diverse branching factors, offering a nuanced representation of relationships in various applications.  

These trees are particularly useful in scenarios where entities have multiple dependencies or associations, such as representing hierarchical file systems, organisational structures, or syntax trees in computer science. 

The structure of an N-ary Tree supports efficient storage and retrieval of information, with each node potentially branching into a variable number of child nodes. While the specific use case often dictates the choice of N, common values include 2 (binary trees), 3 (ternary trees), and higher values for more complex relationships. 

Implementing operations on N-ary Trees, such as traversal or searching, involves adapting algorithms to handle the varying number of children for each node. Despite this additional complexity, N-ary Trees provide a valuable tool for representing and navigating hierarchical relationships in various applications, showcasing their adaptability and versatility in data structure design. 

8) B-Tree 

A B-Tree, short for Balanced Tree, is a self-balancing search tree data structure renowned for its efficient handling of large datasets and optimal performance for disk storage systems.   

Characterised by a variable number of children per node, a B-Tree maintains balance through controlled splits and merges, ensuring a uniform depth. This balance facilitates efficient search, insertion, and deletion operations with a predictable logarithmic time complexity.  

Commonly employed in databases and file systems, B-Trees excel in scenarios requiring rapid access to sorted data and support for dynamic updates. The ordered structure allows for range queries and sequential access, making them particularly suitable for indexing, file organisation, and database management. A good understanding of Python Data Structures can further enhance your ability to implement and utilize B-Trees effectively in various applications.    

Moreover, the adaptability of B-Trees to different scenarios and their ability to optimize I/O operations underscore their significance in the design of robust and high-performance storage systems. 

Conclusion 

In conclusion, understanding the diverse Types of Trees in Data Structure is paramount for any programmer. From Binary Trees to B-trees, each type offers unique advantages, contributing to the efficiency and elegance of algorithms. Embracing this knowledge empowers developers to navigate and optimise complex Data Structures effectively. 

Perform basic operations on data with algorithms by signing up for our Data Structure and Algorithm Training now!