We may not have the course you’re looking for. If you enquire or give us a call on +1 7204454674 and speak to our training experts, we may still be able to help with your training requirements.
Training Outcomes Within Your Budget!
We ensure quality, budget-alignment, and timely delivery by our expert instructors.

Ever wondered how much water fits in a perfectly round beach ball? Or perhaps you're baffled by the calculations needed to design a spherical spaceship? The answer lies in a powerful mathematical concept: the Volume of a Sphere. This seemingly complex idea unlocks the secrets of any object perfectly round.
This blog dives deep into understanding the Volume of a Sphere, offering a detailed explanation that goes beyond memorising a formula. We'll unveil the logic behind the volume equation, explore real-world applications, and equip you with the tools to solve any spherical volume problem with confidence!
Table of Contents
1) Formula for the Volume of a Sphere
a) Volume of Solid Sphere
b) Volume of Hollow Sphere
2) Example for Volume of a Sphere
a) Example 1: Volume of a Sphere given the radius
b) Example 2: decimal radius
c) Example 3: volume of a hemisphere
3) Applications of the Volume of a Sphere
4) Conclusion
Formula for the Volume of a Sphere
Spheres, with their perfect roundness, are essential shapes in science, engineering, and even everyday life. Understanding their volume is crucial for tasks like calculating the amount of paint needed for a globe, the capacity of a spherical water tank, or even the volume of a basketball.
Volume of Solid Sphere
A solid sphere is a three-dimensional object where all the points on the surface are equidistant from the center. The formula for the volume of a solid sphere is the same as mentioned above:
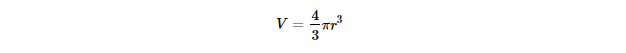
This equation means that to find the volume, you need to:
a) Cube the radius (r3).
b) Multiply by π.
c) Multiply by 4/3.
Example: If a solid sphere has a radius of 5 units:
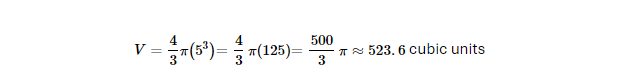
Volume of Hollow Sphere
A hollow sphere, also known as a spherical shell, has an inner radius (r1) and an outer radius (r2). The volume of a hollow sphere is the difference between the volume of the outer sphere and the volume of the inner sphere.
The formula for the volume (V) of a hollow sphere is:
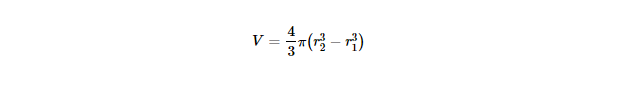
Where:
a) r2 is the outer radius.
b) r1 is the inner radius.
Example: If a hollow sphere has an outer radius of 6 units and an inner radius of 4 units:
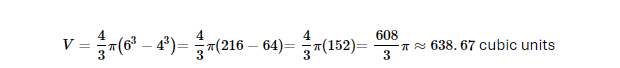
Unlock your potential! Register for our Personal Development Courses today to enhance your skills, boost your confidence, and realise your goals.
Example for Volume of a Sphere
Example 1: Volume of a Sphere Given the Radius
Suppose you have a sphere with a radius of 7 units. To find the volume:

So, the volume of the sphere is approximately 1436.76 cubic units.
Example 2: Decimal Radius
For a sphere with a decimal radius, the process remains the same. Let’s consider a sphere with a radius of 3.5 units.

Thus, the volume of the sphere is approximately 179.59 cubic units.
Example 3: Volume of a Hemisphere
A hemisphere is half of a sphere. Therefore, to find the volume of a hemisphere, you take the volume of a full sphere and divide it by 2. The formula for the volume (V) of a hemisphere with radius (r) is:
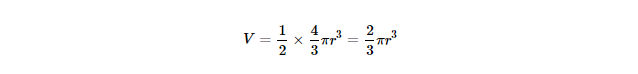
Example: If a hemisphere has a radius of 4 units:

Thus, the volume of the hemisphere is approximately 134.04 cubic units.
Applications of the Volume of a Sphere
Here are 3 applications of the Volume of a Sphere:
1) Calculating Material Needs: The volume formula helps determine the amount of material needed for spherical objects. This applies in construction (concrete for spherical water tanks), manufacturing (metal for ball bearings), or even cooking (batter for round cakes).
2) Resource Measurement: Spheres are all around us! Scientists use volume to estimate resources like the amount of water in a spherical water droplet or the volume of oil in a spherical oil reserve. Knowing the volume helps us manage these resources effectively.
3) Engineering & Design: Spherical shapes are used in many engineered objects due to their efficient design. Engineers might use the volume formula to calculate the capacity of spherical pressure vessels, the volume displaced by a submarine, or even the volume of air a spherical parachute can hold.
Sharpen Your Skills. Train to Become a Top Engineer with our Engineering Skills Training now!
Conclusion
In conclusion, calculating the Volume of a Sphere and hemisphere is straightforward with the formulas provided. Whether dealing with solid, hollow, or partial spheres, understanding these calculations is essential for various practical applications in geometry and engineering. Accurate volume measurement enhances our ability to design and analyse three-dimensional objects effectively.
Take charge of your future! Join our Career Development Course today and unlock the skills and strategies to advance your professional journey.
Frequently Asked Questions

The rule for a sphere's volume is V = (4/3)πr³, where V is volume, π (pi) is a constant, and r is the sphere's radius.

The formula relates the sphere's volume to its perfectly round shape. Imagine stacking many tiny pyramids together to form a half-sphere. The formula calculates the volume of those pyramids, giving the sphere's total volume.

No, spheres don't always maximise volume! For a given amount of material, a sphere is efficient, but a cylinder can hold more volume with a flat top and bottom. Think tall cans versus round balls.

The Knowledge Academy takes global learning to new heights, offering over 30,000 online courses across 490+ locations in 220 countries. This expansive reach ensures accessibility and convenience for learners worldwide.
Alongside our diverse Online Course Catalogue, encompassing 17 major categories, we go the extra mile by providing a plethora of free educational Online Resources like News updates, Blogs, videos, webinars, and interview questions. Tailoring learning experiences further, professionals can maximise value with customisable Course Bundles of TKA.

The Knowledge Academy’s Knowledge Pass, a prepaid voucher, adds another layer of flexibility, allowing course bookings over a 12-month period. Join us on a journey where education knows no bounds.

The Knowledge Academy offers various Personal Development Courses, including the Engineering Skills Training, Time Management Training and the Supervisor training. These courses cater to different skill levels, providing comprehensive insights into Best Courses After 12th.
Our Business Skills Blogs cover a range of topics related to Personal Development, offering valuable resources, best practices, and industry insights. Whether you are a beginner or looking to advance your Engineering skills, The Knowledge Academy's diverse courses and informative blogs have got you covered.
Upcoming Business Skills Resources Batches & Dates
Date
 Engineering Skills Training
Engineering Skills Training
Fri 17th Jan 2025
Fri 21st Feb 2025
Fri 4th Apr 2025
Fri 6th Jun 2025
Fri 29th Aug 2025
Fri 24th Oct 2025
Fri 26th Dec 2025







 Top Rated Course
Top Rated Course



 If you wish to make any changes to your course, please
If you wish to make any changes to your course, please


